曲線の測定と描画

曲線を描画する目的

今までは直線を分割したり、何倍かしてその位置を求めることをしてきました。
これらは「部分のおよその位置」をつかむための方法で、実際には人体はほぼすべて曲線でできています。

実際に人体を描画するときは、まずは直線によっておよその位置を計算し、紙に描いていきます。
ただしこれは位置を取るための下書きであって、本線ではありません。できあがったら最後は消します。

これら直線を元に、実際には曲線を描いていくわけです。だから曲線の性質についても、よく知っておかなければなりません。

曲線の測定と描画

曲線の長さを計測するのは簡単ではありません。
世の中には曲線定規というものもありますが、直線定規よりも精度が悪く、計測に時間もかかります。
さらに対象物の「曲線そのものの長さ」がわかっていても、実際に描画するとなるとやはり曲線定規が必要になってしまいます。
それでは精度が悪いし、あまりに非効率です。なので「曲線そのものの長さ」は測定する必要もなく、知る必要もありません。

そこで、やはり直線だけで考えることにします。
たとえばこのような点を二つとった場合です。2つの黒いバツ印から赤いバツ印の割合を求める場合、

画像：曲線の2つの端に黒いバツ印、中央に一つ赤いバツ印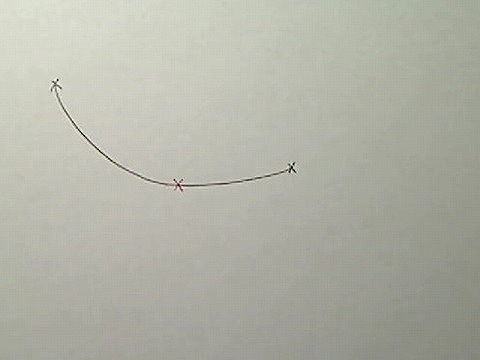

このような場合、赤いバツ印に向かって、縦方向にいくら、横方向にいくら、と長さを出します。

画像：中央の赤いバツ印へ横、縦と割合を測定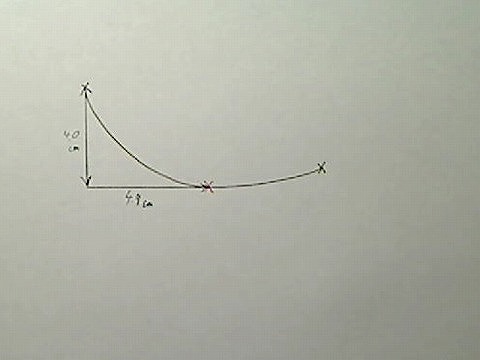

このようにして曲線の中の特徴的な場所をチェックし、そこで分割します。「その点は全体の中の何割」というのを、縦と横でそれぞれ求めるわけです。
分割点を知るだけでなく、これらを参考に線を引くときでも、縦に何分の1、横の何分の1、と測ってポイントを出します。

ところでそういう分割点は、どういう場所がいいでしょうか。
これは目で見てわかりやすいように、「極大」あるいは「極小」点、そして「曲率」の急に変化する点を取るようにします。

曲率

線の曲がり方の強い場所を「曲率が高い」と呼びます。逆を「曲率が低い」といいます。

画像：曲線の曲率の高い部分(A)と低い部分(B)。いびつな曲線。

Aの付近は急カーブなので「曲率が高い」、Bの付近はカーブが滑らかなので「曲率が低い」となります。

極率の変化部分に目印をつけておくと、正確に曲線を描きやすくなります。何も目印がなくて適当に描いてしまうと

画像：曲率一定の曲線を描いてしまった例。先ほどの曲線が裏面に薄く描いてある。

このようになってしまいます。極率の変化点、いわば「急に曲がる位置」をチェックしておけば、正確な線が描きやすくなります。

画像：曲率の変化点をチェックして描いた曲線。

「急に曲がる地点」や「急に曲がっていたのが急に曲がらなくなった地点」は描画するときのいい目印になります。

極大点・極小点

数学の関数分野で、部分的に数値が最大になる場所を「極大点」、部分的に数値が最小になる場所を「極小点」とよびます。

画像：極大点と極小点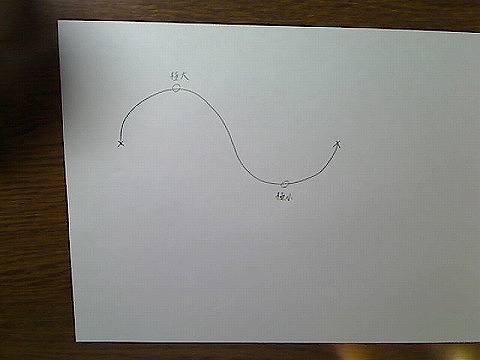

このような場所は曲線を描画する上で一つの基準点になります。
たとえば左右の端だけ目印があると、どのように曲線を描けばいいかわかりません。

画像：極大、極小を無視して描いた曲線。薄く本来の曲線。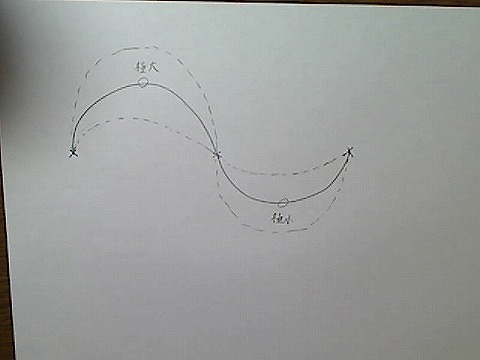

しかし極大、極小点がわかっていれば、それを通るように曲線を描くことで、目的に近い線が描きやすくなります。
極大と極小点も、よい目印の一つです。

曲線の最大太さ

人間の体は全体的には円筒状のものが組み合わさったような形になっています。
そのため部分に「太さ」があることが多く、最大太さをチェックしておくと描きやすくなることが多くあります。

画像：腕の形、最大太さをチェックし、極大点の分割割合を提示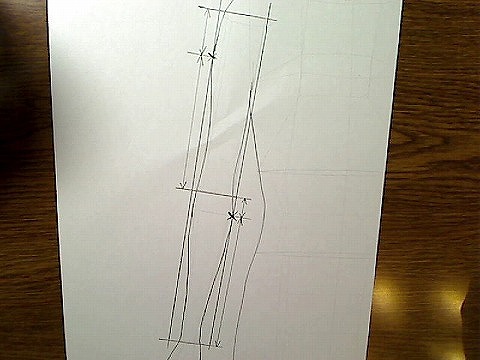

これは簡単に描いてみた腕の形です。このような形を作るとき、図のように最大の太さを基準にし、その中のどの分割割合に最大に太い点があるかを知っておくと、何も見ずに描くときに役に立ちます。