奥行き回転の難しさ
前回は各BOXを平面回転させただけですが、これからはBOXを奥行き回転させる方法について学びます。
しかし困ったことに、奥行きを含む回転をさせたときのBOXの大きさを求めることは、かなり複雑になる場合があり、計算も煩雑になることがあります。
またその理屈の説明も、相当に長くなります。
しかし奥行きを含む回転が難しいのは、BOX理論だけではありません。
ふつうに体を奥行き回転させて描く場合も、特に初心者にとっては難しいものです。
奥行き回転させるとどのような絵になるかというと、たとえばこのような絵になります。
画像:腕を前に突き出している絵とBOX。
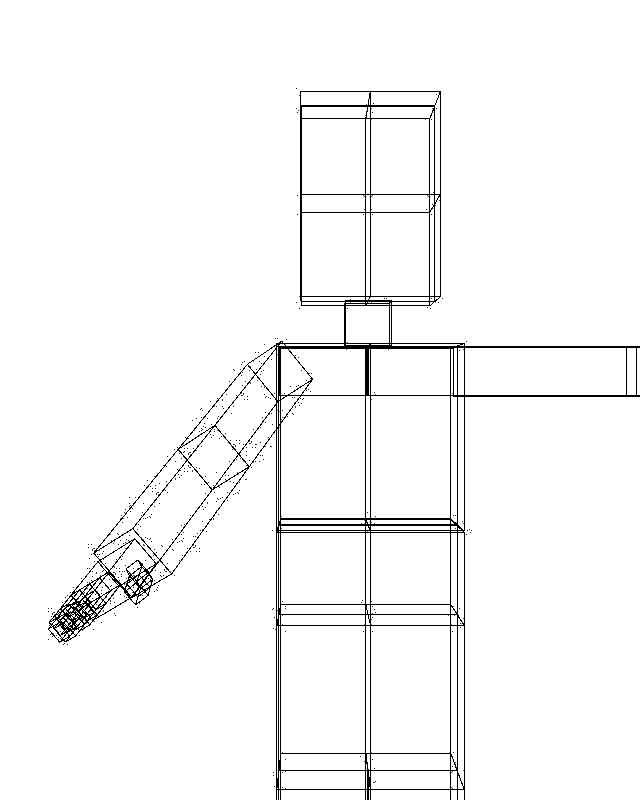
腕をカメラ(こちら側)へ突き出しているようなポーズです。
こういったポーズ、つまりカメラ(絵を見ている人)から見て遠くあるいは近くへ向かっているような形です。
なぜこのような視点が難しいと感じるのかというと、私たちは頭の中で腕の長さがどれくらいなのかを知っており、それを絵の中に無意識に反映させようとしがちだからです。
このような構図で腕の「見た目の長さ」を測ってみると、実際の腕の長さ(24センチ×2)よりもずっと短いことがわかります。
絵に慣れている人はこういったミスはしないかもしれませんが、絵の初心者ですと、頭の中にある腕の長さをそのまま絵に出して、突き出したポーズを描いてしまいがちです。
画像:腕の見た目の長さ48センチで前に突き出した誤った絵。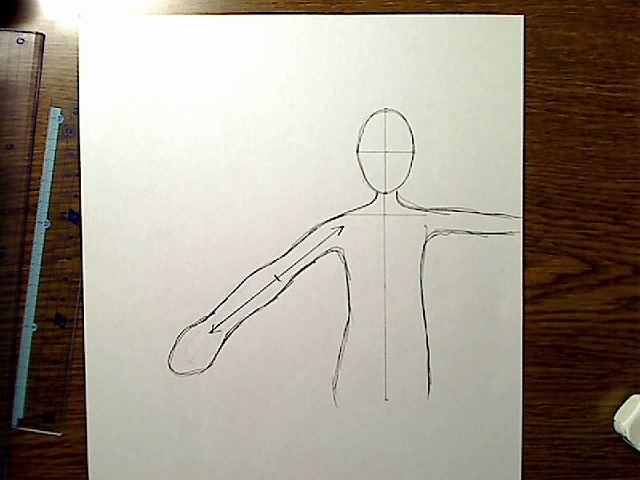
このような問題の簡単な解決法の一つは、サンプリング法を使うことです。これははじめの章で説明したのですが、計算や理屈ではなく、実際にそのようなポーズをした写真を用意したり、自分でそのようなポーズをとって写真に取り、形をそのまま写し取るやり方です。
ただこのやり方ですと「何も見ずに描く」という当サイトの目標は達成できません。
「奥行き」という難しさ
私たちは「絵」というと、二次元的な印象を持っています。つまり画面というのは平面であり、見たまま平面的に描画すればいい、と特に初心者では思いがちです。
しかしながらすべての物体は3次元的にこの世に存在するため、すべての物質には、画面では一見認識できない「奥行きの長さ」というのが存在します。
そしてこの奥行き長さは、描くべき映像を目で見ているだけではわからないのです。
問題を単純にするため、やはりBOXで考えましょう。
一辺が3センチメートルの立方体(面がすべて3センチ×3センチの正方形)があったとします。
これを真正面から見た場合と、斜め45度くらい奥行き横回転させてみた場合とで比較して見ます。
画像:立方体。斜め上から見た図と、真正面から見た図と、45度奥行き横回転させた図。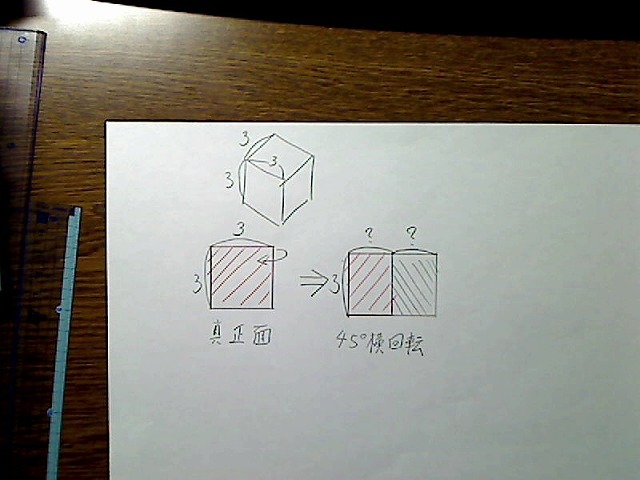
真正面で見たときの縦の辺の長さは変わっていませんが、横の辺の長さは回転後に斜め奥へ向かっているため、見た目の長さは変わってしまいました。回転前より短く見えます。
辺の実測値は3センチでわかっているのですが、斜め奥へ伸ばしたときの、この「見た目の長さ」は、一見してどれくらいかわかりません。
さらに回転後、今まで見えなかった辺が見えてきています。回転前はまっすぐ奥へ伸びていたために見えていなかった右の面が見えてきています。この面の辺は回転前は見えていなかったので、どれくらいの長さかわかりません(実測値は3センチですが、やはり奥行きを伴っているので見た目の長さがどれくらいかはわかりません)
このように奥行きを伴って回転させると、見た目の長さが変わってきます。この長さがわからないために、正確に描画するのが難しくなってきます。
しかしこれも計算で、かなり正確に出すことができますので、これからやっていきましょう。
BOX理論で立体を理解する
BOX理論という難しそうな名前をつけましたが、BOXとは要するに体の部分の概形のことなのです。
BOX理論でなくても、体を描くときにまずおよその形の見当をスケッチとして下書きする、というようなことは、絵を描く人ならふつうにやることでしょう。
ところで絵、特に人物画というのは、数をこなせば上手くなると考えている方もいるかもしれません。
しかしそれは場合にもよります。同じポーズばかり、しかも何も考えずに描いてばかりでは、見たことのないポーズには対応できないのです。
たとえば胴体を正面から見た絵ばかり100回描いても、胴体を真上からみた形がどんなふうになっているかはわからないままです。
ある視点から見た絵だけではなく、あらゆる方向から見た絵を描けるようになるには、立体として形状を把握していることが必要です。
それでも何の下書きもなしに、いきなり真上から見た絵を描けといっても、慣れていないとなかなか形が想像できません。
無理に慣れていない形を想像し、手の動くままに描いてしまうと、出来上がった形はやはりおかしなことになっている、ということは少なくありません。
そこでBOXのような概形を最初に描いてしまい、そこから基準となる線など(関節点や目立つ凹凸など)を描いて、さらに詳細を書き込んでいく、という手順にすると、速く、しかも問題があまり起こらずに仕上げることができるようになります。
BOX理論をそのまま使わなくても、概形をつかんでから描く練習をしておくと、あまり迷わなくてすむようになっていきます。