簡単な奥行き回転
いきなり全身を書くのは難しいので、まずは単一のBOXを回転させたときにどのような長さになるかを追求していきましょう。
単一のBOXを回転させたときの各辺の長さの出し方を知っていれば、全身を描く場合はそれを繰り返して仕上げるだけです。
ためしに頭部のBOXだけ考えてみます。
まず各辺の絶対長さを示しておきます。これは各辺の本当の長さであり、「見た目の長さ」ではありませんので注意してください。
画像:斜め上から見た頭部BOXのみ。各辺の絶対長さだけ示す。目と鼻を口を簡単に描画。
そして頭部を正面に見たときの長さは次のとおりです。単位はモジュールです。
画像:頭部BOXのみ、正面図、長さはモジュール目と鼻と口を簡単に描画。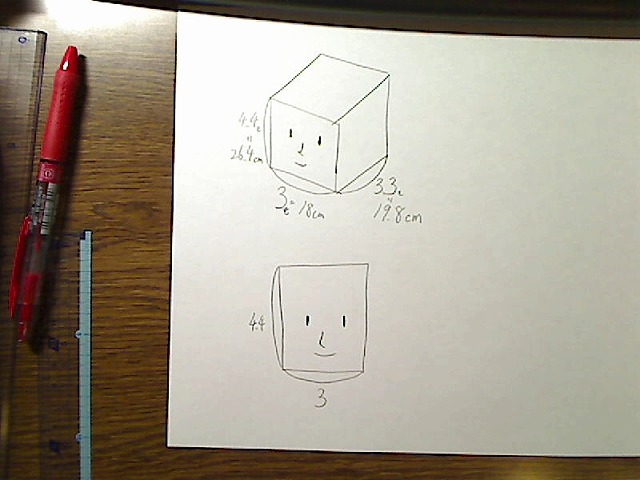
さて、これを見た目左へ30度回転させてみます。するとこんな形になります。
画像:奥行き回転左向きへ30度した図。横の辺、頭部の幅をa、奥行きをbとする。
頭部の幅は先ほど3だったのですが、少し短くなりました。その長さをaとします。
頭部の奥行きは3.3です。先ほどはこの奥行きの線は見えていませんでしたが、回転したのでこの線が見えてきました。この長さをbとします。
さて、aとbの長さはどのように出せばいいでしょうか。
まずこれを真上から見るとどうなるかを考えて見ましょう。
画像:回転前と回転後、真上から見た図と先ほどの図。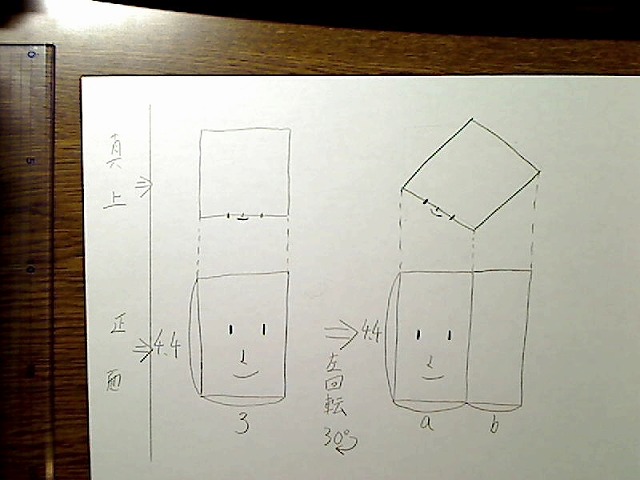
真上から見るとこんな感じです。まず辺aについて考えてみましょう。
頭部の横幅を回転前、真上から見ると横一直線で3の長さでした。30度回転後にはこのようになります。
画像:横幅3を30度回転させた図。回転中心は同じ。回転後の長さも3。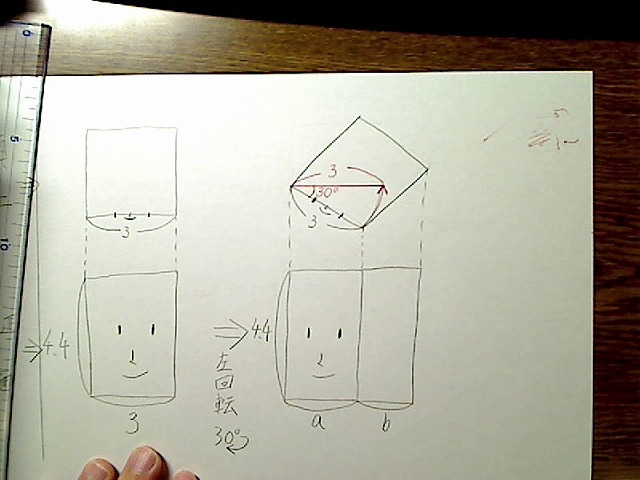
回転後の見た目の長さ(カメラから見た「見た目の長さ」)は、
画像:回転後aの回転前aに下ろした垂線から回転中心までの長さをa。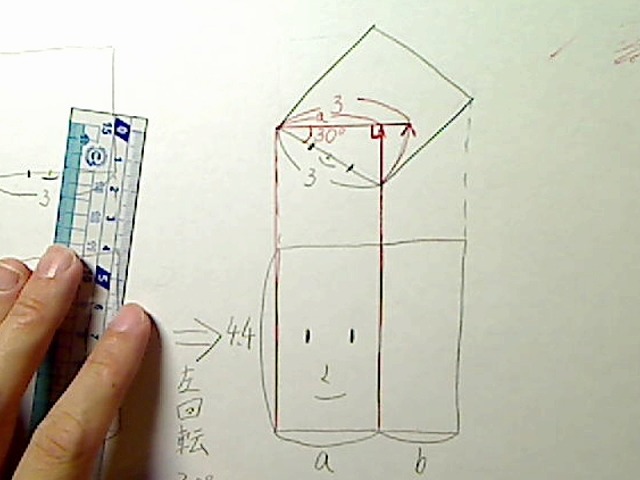
このように、回転前の線に垂直に線を下ろし、その交点と回転中心までの長さが、求めるべきaの長さとなります。
そしていきなり結論をいいますと、aの長さは「3×0.85倍」になります(正確にはa×0.866倍ですが、この数字は覚えにくいので0.85あるいは85%と覚えておくと便利です)
30度回転させている場合は、必ずこの値になります。これは数学で「三角関数」というもので、通常高校で習う内容です。
次の章では三角関数の基本的なところを説明していきます。
しかしここでは絵を描くことが目的なので、完全に理解したり応用問題を解く必要などはありません。
また「数学は苦手だ。何を言っているのかさっぱりわからない」という場合でも、絵に応用する場合は大丈夫です。上述で「30度回転させると0.85倍」という値を出しましたが、このように「何度回転させると何倍になるか」かという値を暗記するだけでもいいのです。
理屈がわからなくても何度か間隔をあけて倍率を覚えておくだけでも応用はできます。「15度では0.95倍、30度で0.85倍、45度で0.7倍……」などと暗記しておくだけでも十分です。
しかし数学的な原理を理解していないよりは、理解しているほうがさまざまに数学的応用が効きますし、いろいろと有利です。