絵と数学の関係
突然数学の話になってしまいますが、絵というのは本来数学と密接に関係があるものです。
もう少しいうと、美術というより設計図を描くような場合、数学を知らずに描くことはできません。
透視図法や遠近法というのも、本来は数学的な問題と関連付けて考えるほうが深く理解でき、応用も利かせることができるようになります。
また3DCGでアニメーションを作るときは、数式を使ってアニメーションを作ることがあります。
数式を使わなくても、グラフを見ながら数字をいじることはよくあります。
美術を志すのであれば、数学を知っていたほうが有利です。
美術でなくても、たとえばゲームを作るときに、アニメーションを作るときにプログラムに現実の物理法則をそのまま適用することがあります。
数学や物理などの理系科目は、単一のイラストだけではなく、特にアニメーションさせるときには重要になることがあります。
三角関数とは?
まずこの図を見てください。
画像:直角三角形、斜辺がa、底辺がb、もう一つの辺がc。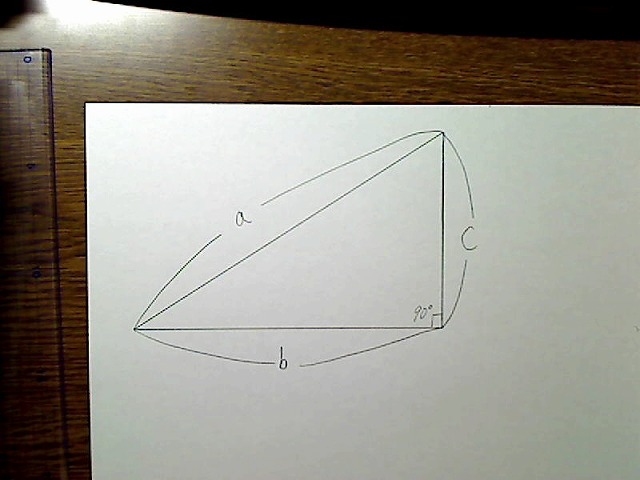
三角形のうち、内角の一つが直角(90度)であるものを直角三角形と呼びます。
今の場合、その直角部分は図のように右下か左下のあるとします。
また辺にも呼び方があり、直角三角形の斜めの辺を「斜辺」、下の横の辺を「底辺」、さらにもう一つ縦の辺があります。
それで今回は、図のように斜辺の長さをa、底辺の長さをb、残りの縦の辺の長さをcとします。
そして内角のうち、底辺と斜辺の角度をθ(シータ)としましょう。この記号は数学の授業でもよく使われます。
画像:底辺と斜辺の角度をθ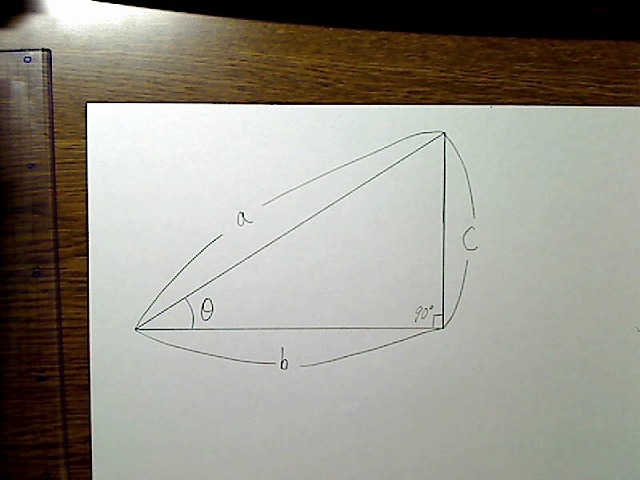
このとき
sinθ=c/a
cosθ=b/a
tanθ=c/b
となります。これが三角関数です。
呼び方ですが、sinは「サイン」、cosは「コサイン」、tanは「タンジェント」です。
たとえばθが30度のとき、cosθはb÷aになります。
たとえばa=5、b=4、c=3とすると、cosθは4÷5で0.8になります。
角度によってsin,cos,tanの値は一つに決まる
さて三角関数で重要なことは、角度によってそのsin,cos,tanのそれぞれの値は、一つに決まるということです。
たとえばsin30度は0.5です。これは辺の長さがどんな組み合わせでも変わりません。θが30度の場合、c/aは必ず0.5という値になるのです。ほかの値になることは絶対にありません。
(条件に注意してください。直角三角形の場合で、図のようにcos(底辺÷斜辺)を決めると、このように一つに決まるということです)
ちなみにある角度のsin,cos,tanの値を知りたければ、Windowsに最初から付いている電卓を使ってもわかります。
Winodowsで「すべてのプログラム」「アクセサリ」「電卓」を立ち上げ、「表示」のところで「関数電卓」を選び、「3」「0」「sin」と順番に押すと、sin30度の値がわかります。0.5と出ます。
なおこれは覚えなくてもかまいませんが、これらの図形を見てもわかるとおり、それぞれの三角関数には関連性があります。
たとえばsinθ=cos(90-θ)です。sin30度=cos60度になります。
またtanθ=sinθ/cosθなどの法則もあります。これらは難しい数式を使わなくても、図形を見てみればわかることです。
三角関数は直角三角形のみに適用
三角関数は直角三角形の場合にのみ当てはまるので、直角三角形でなければこれらは当てはまりません。たとえば
画像:直角三角形ではいただの三角形。斜辺がa、底辺がb、残りの辺がc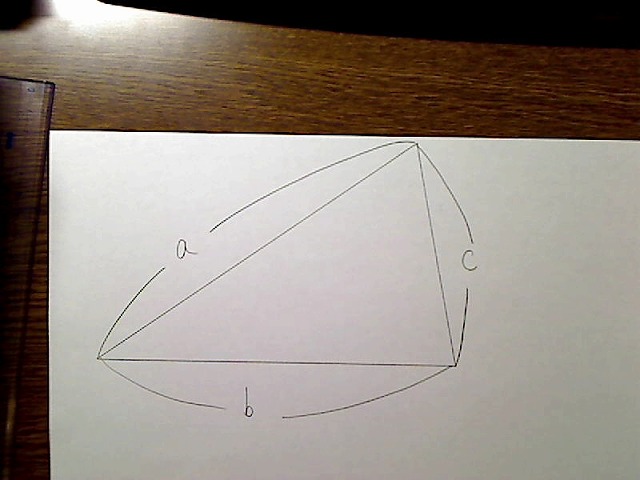
こんな三角形でb/aを求めても、cosにはなりません。あくまで直角三角形の場合のみです。
対称図形でも同じ
直角部分は右下でなくてもいいのです。たとえば左下でもいいし、上下対称でも同じです。
画像:先ほどの直角三角形を上下と左右に対称の図形。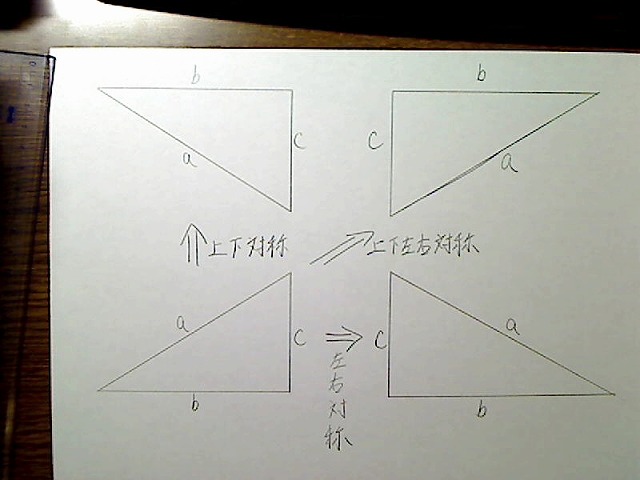
このような三角形でもcosθ=b/aのようになります。
cos45度の値を求めてみる
もう少し例を出してみましょう。直角三角形で、底辺と斜辺ではさまれている角度を45度とする三角形を描いてみます。
画像:直角三角形で斜辺と底辺の角度が45度。斜辺がa、底辺がb、残りの辺がc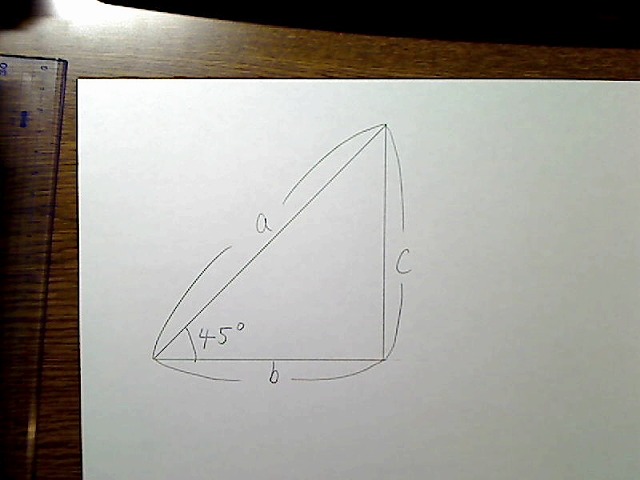
先ほど三角関数の値は角度によって一つに決まるといいました。cos45度の値は一つしかありません。0.7です(正確には1÷√2ですが)
cos45度が0.7なので、たとえばaの長さが1だとすると、底辺の長さはa×0.7=1×0.7で0.7となります。
aの長さが2だと、底辺は2×0.7で1.4となります。
もう少しいうと、直角三角形の場合で、3つの内角のうち直角以外の一つの角度の大きさを決めてしまうと(たとえば図のθの値を決めてしまうと)、ほかの辺の長さもすべて自動で決まる、ということです。
三角形に関するほかの法則
自動で長さが決まってしまうというのは、不思議に思われるかもしれません。
しかし数学には、たとえば三平方の定理(ピタゴラスの定理)というのがあり、直角三角形では斜辺の2乗はほかの2つの辺の2乗の足し算であるという法則があります。
画像:直角三角形で底辺が3、縦の辺が4の長さ。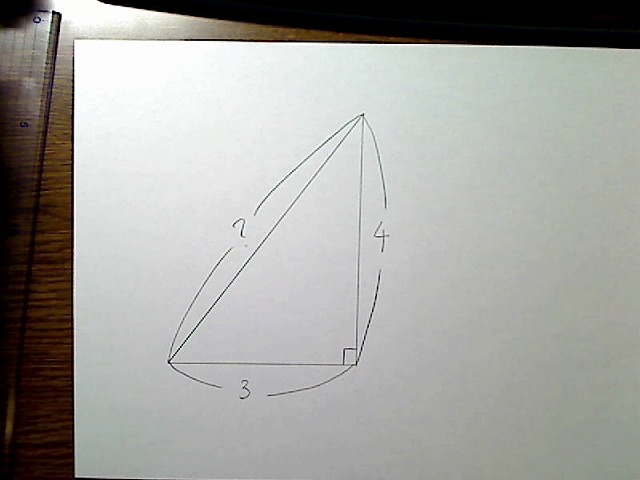
このような三角形の場合、斜辺の長さは3の2乗+4の2乗=9+16で25になります。これは5の2乗なので、斜辺の長さは5になります。
また三角形は、「三角形が一つに決まる条件」が3つあり、「1辺とその両側の2つの角度が決まる」「2辺とその間の角度が決まる」「3辺の長さが決まる」というのがあります。
三角形は、一つの辺を決めるとそのほかの辺の長さが自動で決まる場合がたくさんあります。
さらに三角形は、内角の合計が180になるという法則もあります。三角関数の説明では直角三角形のみ扱いますが、直角三角形なのでまず一つの角度は90度なので、残り2つのうち1つの角度を決めると、最後の角度も自動で決まります。
内角3つをすべて決めてしまうと、一つの辺の長さを設定すれば三角形の形は一つに決まります。つまり一つの辺の長さを決めると、残り2つの辺の長さもすべて自動で決まります。
もう少しいえば、三角形を描くときには、この法則を知らないと思うような長さで描けないという意味でもあります。
たとえば斜辺を2、底辺を1の長さで直角三角形を描きたいとき、その間の角度を30度にすることはできません。ここの角度は必ず60度になるからです。無理やり60度にすると、斜辺2、底辺1の長さにはならなくなります。