三角関数の使い方
さて美術でどうやって三角関数を使うかです。まずはこの図を見てみましょう。
画像:ある横の線(長さa)とその30度回転後の線を描く。長さは同じ。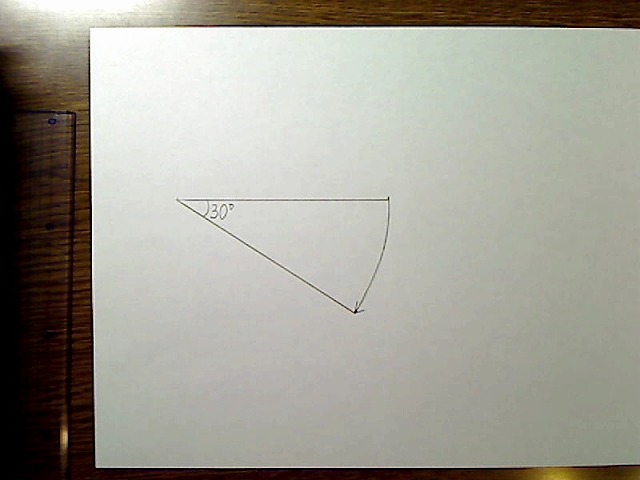
ある横一直線の線があります。これを少し回転、たとえば30度回転させるとこのようになります。もちろん長さは同じです。
この横一直線は、BOXを真正面から見た横の幅の長さに相当します。
さて、回転後の線の一つの端から、回転前の線に向かって垂直に線を下ろします(垂線を引く、といいます)
この交点と回転の中心までの長さをbとしましょう。図で表すとこのようになります。
画像:垂線との交点から回転中心までの長さをbとする。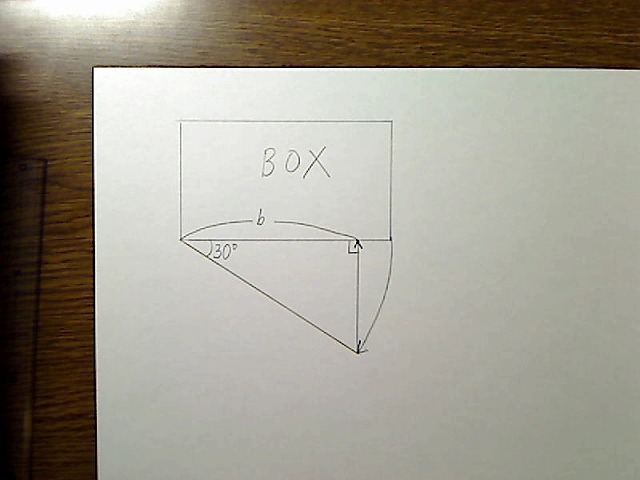
このbの長さこそ、BOXの横の線を30度回したときの「見かけの長さ」なのです。
ここで三角関数が使えるわけです。垂線を下ろしたので、bとa、さらに垂線の3つの辺で三角形を作ると、ちょうど先ほどの説明と同じ直角三角形になります。
画像:直角三角形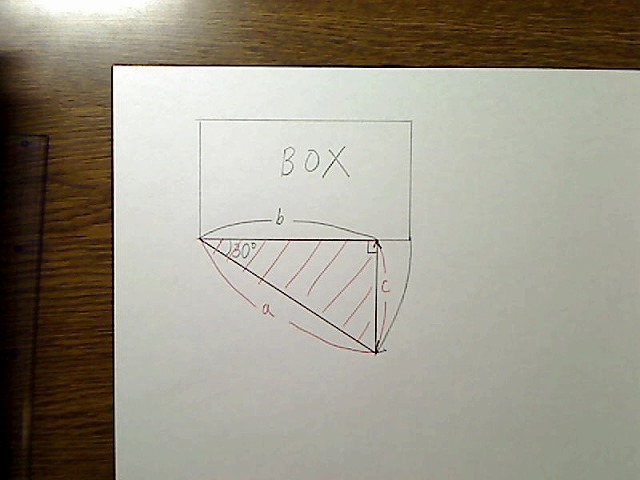
aの長さがBOXの横幅なので、bの長さは「a×cos30度」で決まるわけです。cos30度は約0.85です(正確には0.866……ですが、美術であまり細かい値を使ってもしかたないので、およその計算しやすい、覚えやすい値でやることにします)
画像:計算後の値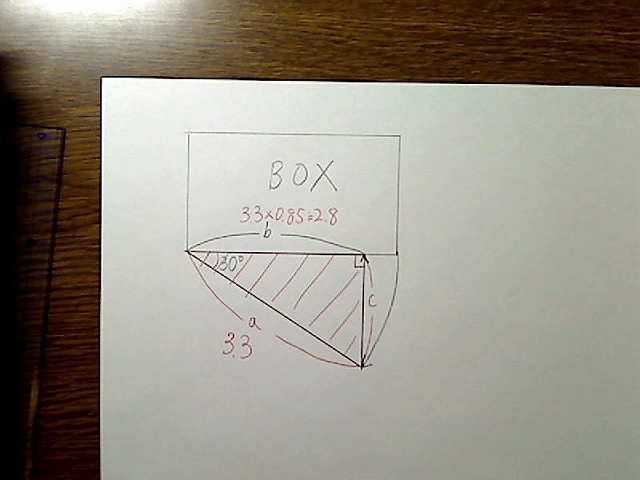
なので、たとえば頭部の横幅は3.3モジュールですが、頭部を横にこのように30度回転させたときの横幅は、3.3×0.85でおよそ2.8になります。
計算しなくても「横の線のだいたい0.85倍」と覚えてその長さを目で測って線を引いてもかまわないわけです。0.85というと、全体の長さのおよそ6分の5あたりです。元の長さの6分の1の長さを切り取ればおよそ正確な回転後の長さになります。
ためしに計算して描いてみる
ここで一つ、キャラクターの頭部のBOXを奥行き方向へ横30度に回転させた場合の長さを出して、BOXだけ紙に描いてみましょう。
はじめに頭部BOXの各辺の長さ(見た目ではない本当の長さ)を確認しておきます。
画像:頭部BOXの各辺の絶対長さ、斜め上図。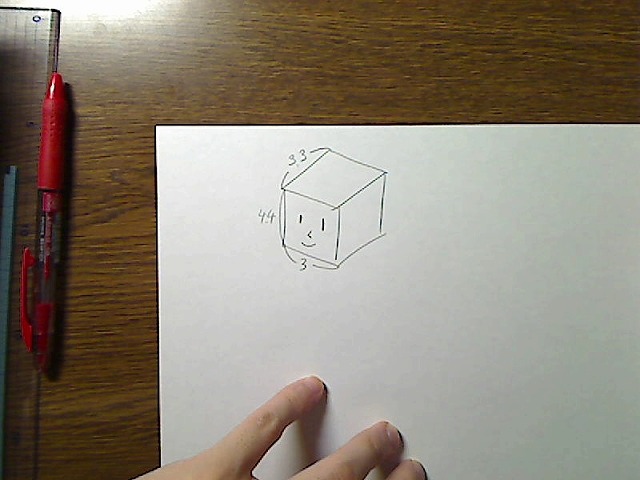
これを真正面から見た場合はこのようになります。説明のため、真上から見た図も描いておきましょう。
画像:真正面図と真上図、頭部BOX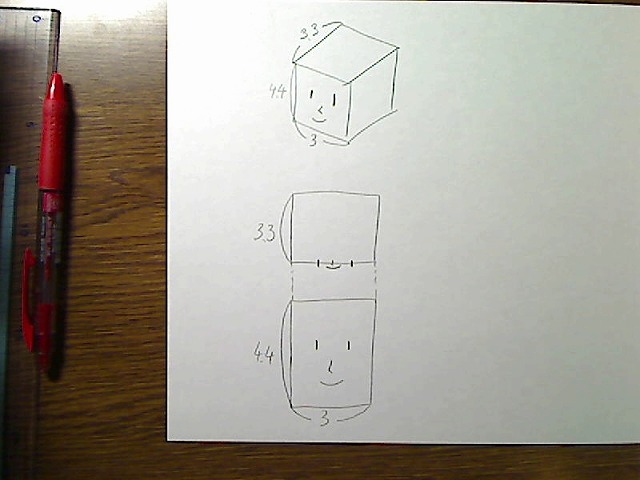
これを左に30度回転させます。すると
画像:先の画像に加えて横30度回転させた図、横幅の見た目の長さはa、奥行き幅の見た目の長さはbとする。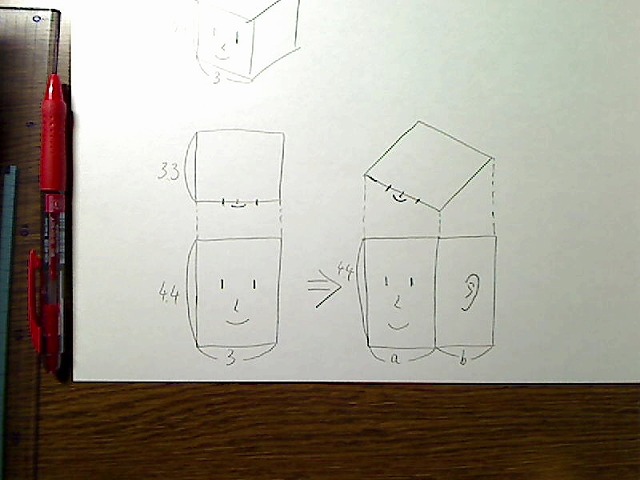
まず正面図のときの横幅3モジュールは、30度回転させたときの見た目の長さaは
「3×cos30度」です。
画像:頭部横幅の見た目の長さaは3×cos30度である説明図。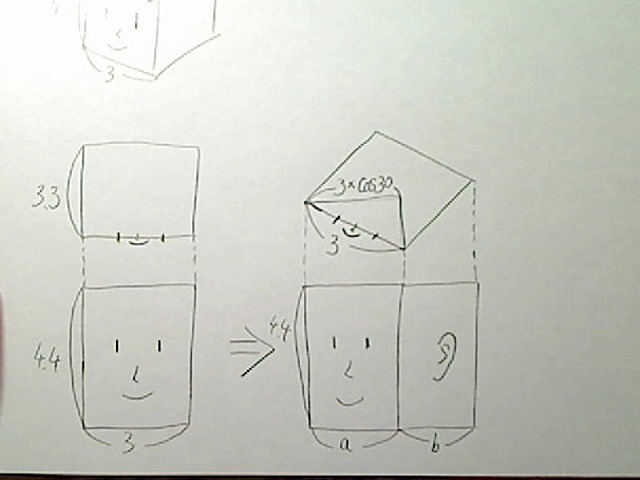
cos30度の値は約0.85なので、3×0.85=2.55、四捨五入で2.6としましょう。
小数点以下、あまり細かい値まで計算しなくても、どうせ定規で目で見て測れる精度には限界があるので、少々いい加減でもかまいません。
a=2.6という長さは出ました。
次に頭部BOXの奥行き幅は3.3モジュールです。これは正面図のときはまっすぐ奥へ向かっていた線なので、見えませんでした(ゼロの長さでした)
しかし回転後はこれが長さを持って見えてきました。ここの長さも計算で求められます。
画像:奥行き幅を×sin30度すると見た目の横幅になる説明図。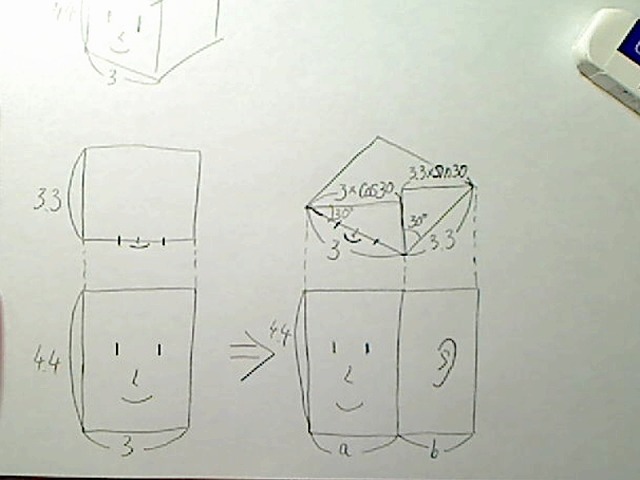
図で説明するとこうです。奥行き幅を30度回転させると、ちょうど三角関数の説明で使った直角三角形を回転させてひっくり返したような形になっていますが、理屈は同じです。
このようになるため、求めるべき長さbは、元の長さ3.3にsin30度をかけた値になります。
b=3.3×sin30度
sin30度は0.5なので、b=3.3×0.5で、1.65、四捨五入で1.7としましょう。
b=1.7
あるいは図のこの角度は90度−30度で60度になるため、
画像:回転角度30度を90から引いた60度の部分。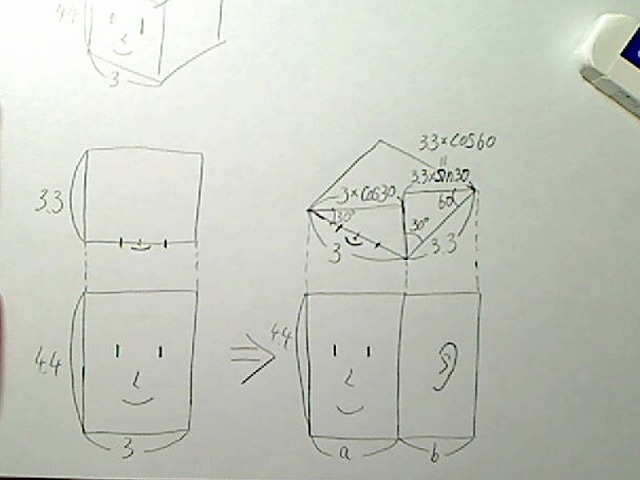
b=3.3×cos60度
でも同じ値になります。実際に三角関数を使うときは、sinやcosの値を覚えておかなければなりませんが、このやり方ならcosの値を覚えておくだけで全部対応できるので、便利です。
これを図で示すと次のようになります。
画像:頭部BOXを左に30度回転した各辺の見た目の長さ。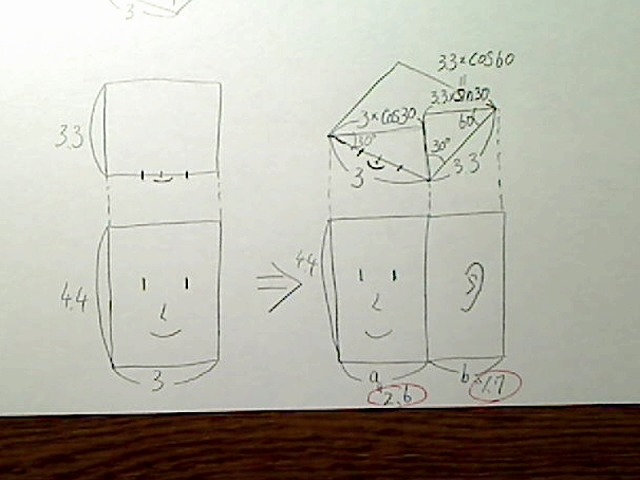
後はいつもどおり、定規で描くだけです。
画像:頭部BOXを作り、輪郭線も書き込んだ絵。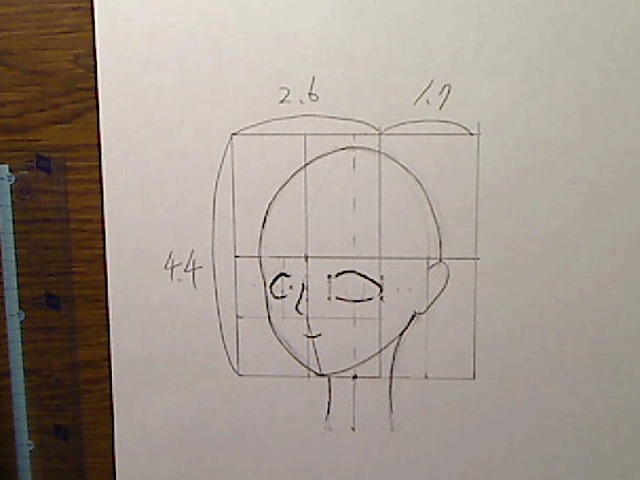
空間的な思考が必要
30度回転したにもかかわらず、奥行き幅の見た目の長さを求めるのに今はcos60度という値を使いました。
これは線が奥方向へまっすぐ伸びていたからであり、空間的に計算して60度という値が出てきたのです。
このように空間的な理屈を知っておかないと、計算を間違うことがあります。何も考えずに「30度回転させたからcos30度で0.85倍すればいい」と覚えていると、とんでもない計算間違いをしてしまいます。
なので数学的な理屈を納得した上で計算するようにしてください。
少々面倒に見えますが、何度もやっていると慣れてきて、すぐに計算できるようになってきます。
多くのBOXでは、一つの辺を×cosθすると、次にはcos(90-θ)することになります。この順番はよく使うので、覚えておくと後が楽です。
これらは近似値である
ここまででとりあえず、BOXを横回転させた場合については描けるようになりました。
しかし実はいうと、これら見た目の長さは完全に正しい値ではありません。
BOXを奥行き回転させたときの見た目の長さは、実際は遠近法によって遠くのものほど小さく見えます。
なので同じ頭部の中でも、カメラより奥へ行くにしたがって、長い線も短く見えるのです。
こういった遠近のない図、つまり「真上から見た図」では遠近が起こらないために、三角関数で正確な値が求められますが、正面からの見た目の長さでは奥のものほど少し短くなり、手前のものほど少し長くなるのです。
しかし実際のところ、そのような遠近による長さの誤差というのは、無視できるほど小さいものです。
これらの長さのゆがみは専門用語で「パースペクティブ」と呼ばれるもので、カメラの位置や画面の枠の取り方によって異なってきます。
これらの説明はまた長くなるので、また後で詳しく説明します。遠近によるこうしたゆがみについては、今はとりあえず考えないことにして話を進めます。