実践
前にすべてのBOXを回転させずに、ひざ立ちの女性の絵を描きました。
こんどは各部のBOXのいくつかを、奥行きへ横回転させて描いてみましょう。特に胴体あたりは横へひねりを加えることによって、ポーズ的にも面白みが出てくると思います。
前回と同じ形ですが、頭部を左へ奥行き45度回し、胴体は胸部が30度程度、腰は15度くらい回し、脚は正面を向いたままにします。腕は前回と同じでいいでしょう。
まずラフスケッチを描いてみます。
画像:ラフスケッチ
次に各部のBOXの見た目の長さを出していきます。
その前に、各部のBOXの各辺の絶対長さ(見た目ではない元の長さ)の確認をします。
画像:各部BOXの各辺の絶対長さを確認。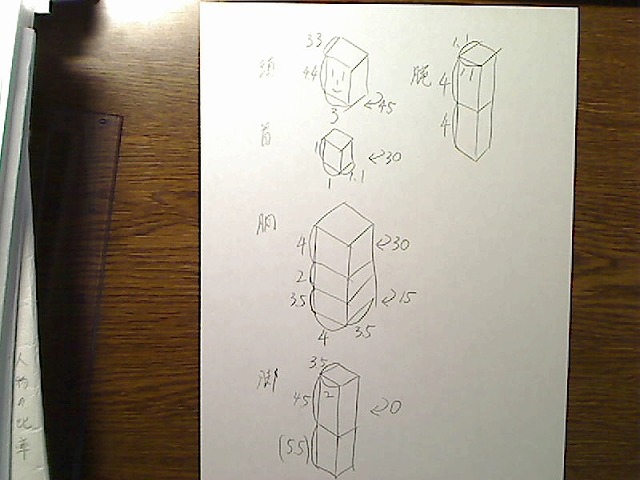
これを元に書く辺の見た目の長さを出していきます。
BOXはたくさんありますが、計算のしかたは同じです。
横幅の見た目の長さは「元の横幅長さ×cos回転角度」
奥行き幅は「元の奥行き幅長さ×cos(90-回転角度)」あるいは「元の奥行き幅長さ×sin(回転角度)」
となります。
これですべてのBOXの見た目の長さを出していきます。
画像:すべてのBOXの見た目の辺の長さ。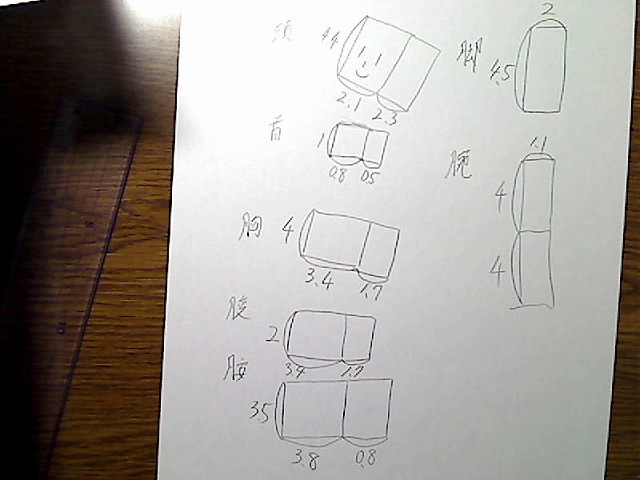
長さを計算し終えたら、次はそれらを紙面に描画していきます。
今回も1モジュールを1センチメートルとして描いていきます。
BOXを描くときの手順ですが、なるべくはじめに「中央線(BOXの中心を縦に通る線)」から描き始めましょう。
後で説明しますが、この中央線は複雑にBOXを回転させるとき(縦横2方向に回転させたとき)には非常に重要になってきます。
また中央線はBOXの三次元的な中心位置となるので、形状を把握し、関節点の位置を正確に描きだすための重要な指標になります。
頭部BOXを、まずは中央線から描いてみます。今回のポーズでは頭部は少し平面的に斜めを向いていますので、中央線を少し斜めに引きます。長さは4.4センチです。
画像:頭部BOXの中央線。
さて頭部の横幅の見た目の長さは2.1センチ、奥行き幅の見た目の幅は約2.3なので、横の全部の長さは4.4センチです。なので中央線から左右にそれぞれ2.2センチ引き、これを2.1センチと2.3センチに分けます。
画像:横幅を分けて頭部BOXを描画。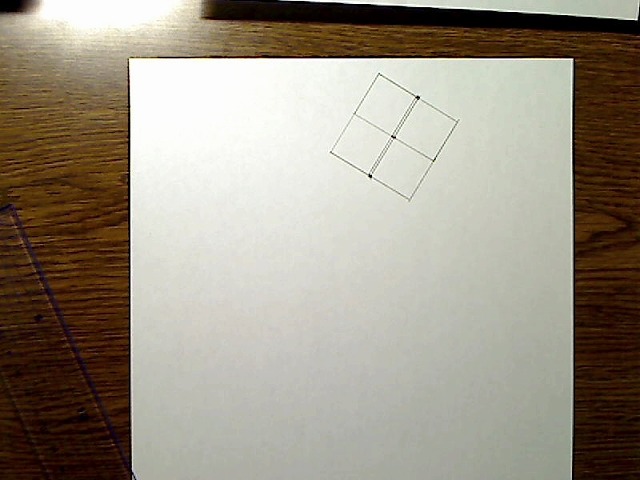
ここから頭部の関節点を出します。ちゃんと立体的に考えます。
画像:頭部の関節点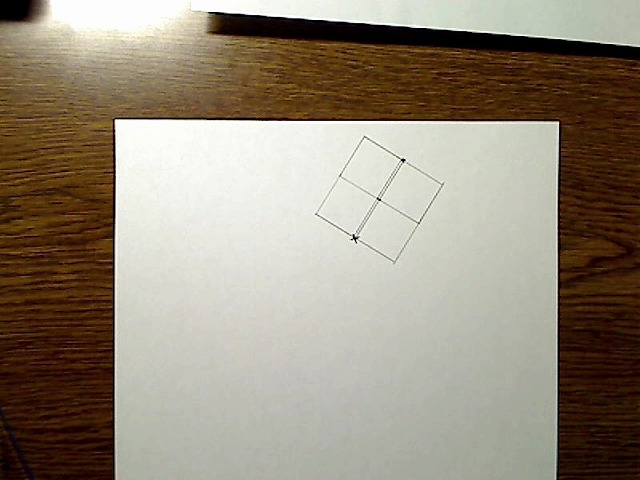
そしてここを首の関節点と一致するように、首のBOXを描きます。
画像:首BOX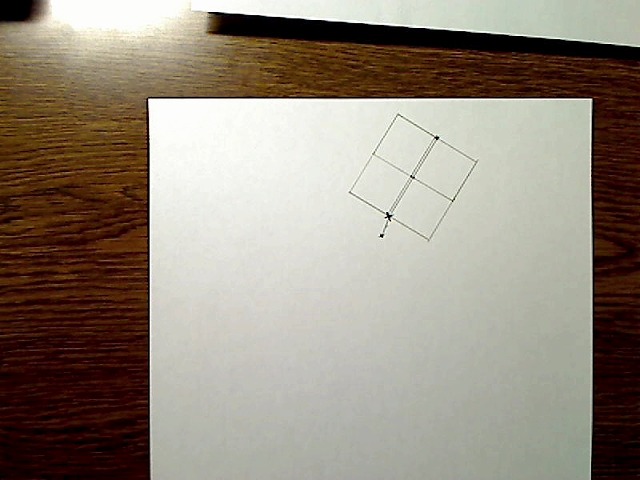
首のBOXも頭部と同じように、最初に中央線を描いてからそれにあわせてBOXを描いていきます。
ほかのBOXも同じ要領で描いていきます。
画像:すべてのBOXを描画。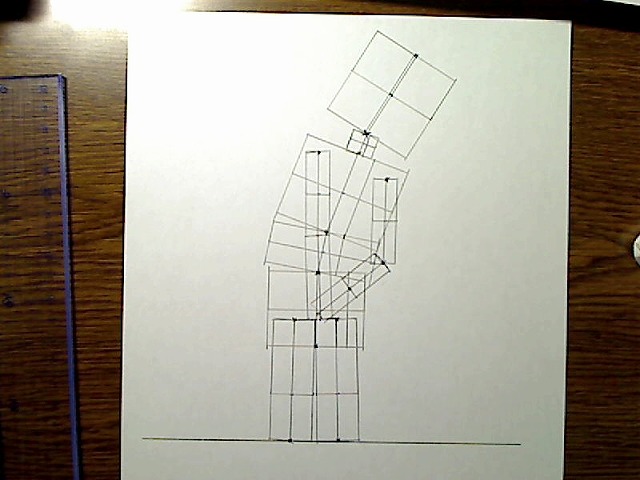
BOXを描いたらそれにしたがって輪郭線を描いていきます。
真正面図で輪郭を描くのは簡単でしたが、BOXに角度が付いている場合は直感で形状を把握しにくくなります。
そこで輪郭線を描く場合、各BOXごとに、3つの回転方向(前屈後屈方向、側屈方向、回旋方向)ごとにそれぞれ下書きの輪郭を描いていくとわかりやすくなります。その輪郭線の下書きを描画した後に本当の輪郭線を描くと、形状を把握しやすく、間違いを起こしにくいです。
画像:輪郭線の本線を描画。
画像:服や髪、顔面パーツなども描画。
奥行き縦回転
さて、ここまではBOXを、真正面図から1回回転させるだけでした。
しかし本来はどのような角度からでも描けなければなりません。これだけではカメラが少し上、あるいは下に下がっただけでも異なる形になってしまいます。
どんな角度のBOXでも描けるようになるには、これよりさらに1回転、縦方向に回転させた場合の各辺の長さを求める必要があります。
画像:BOXを横、さらに縦に1回回転させた図。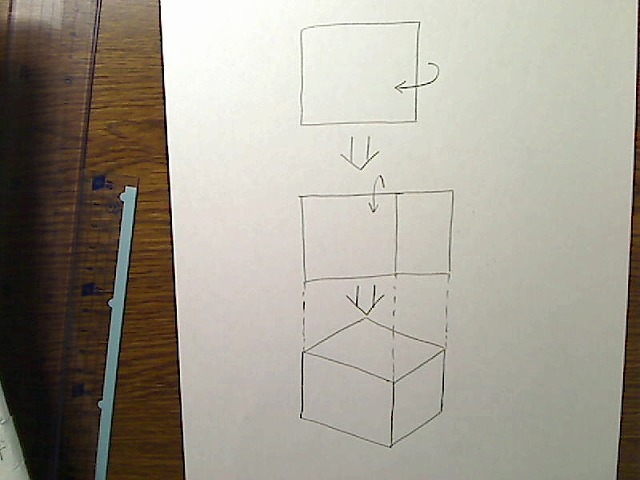
これにさらに、紙面の平面方向に回転させたものを加えれば、どんな方向から見たBOXでも描くことができます。
画像:BOXをさらに平面回転させたもの。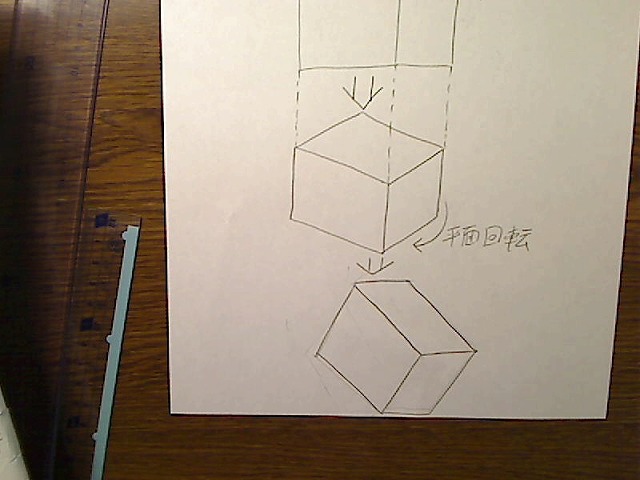
さらに1回、縦方向に回転させたときのBOXの各辺の長さはどのようになるでしょうか?
次の章でそれをみていきましょう。