複雑な角度のBOX理論の実践
これでBOXがどんな角度でも、その見た目の長さを出す計算を学んだので、どんな角度からでも理屈上は描けるはずです。
今回は頭部のみ、斜め上から見た図を描いてみましょう。頭部を横方向(左)に奥行き回転30度、縦方向(下)に45度回転させた図を想定します。
ラフスケッチを描くと、こんな感じになると予想できます。
画像:左30度、下45度回転させた頭部のラフスケッチ。
まずは頭部BOXの各辺の絶対長さを確認しておきます。
画像:頭部BOXの各辺の絶対長さ。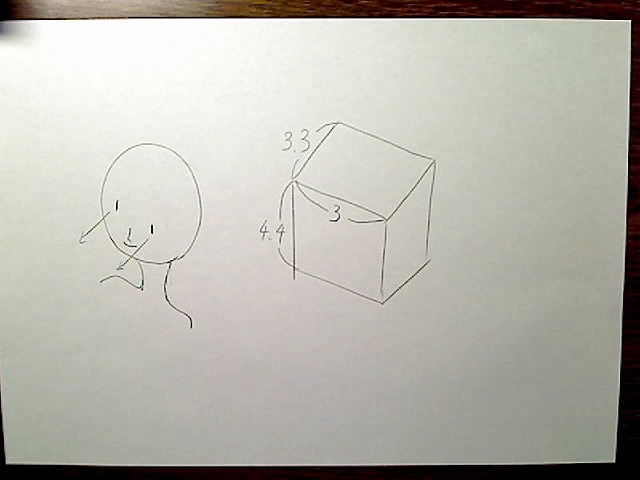
次に真正面から見た図です。それを30度横(左に)回転させ、さらに縦方向(下)に45度回転させます。
画像:頭部BOX、真正面図から左30度、下に45度、順番に回転させる。これらの見た目の長さ。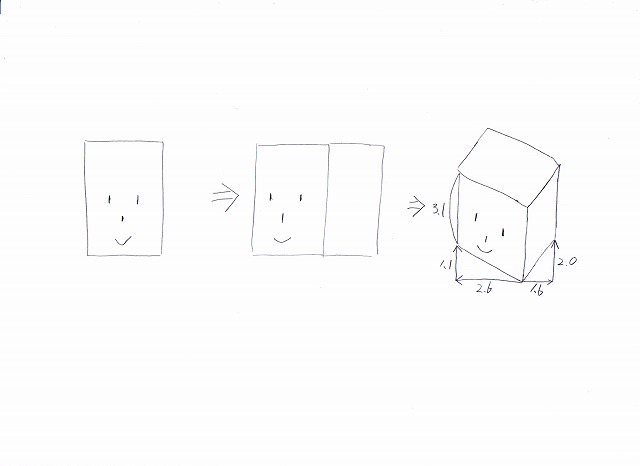
長さがわかったところでBOXの描画に入るわけですが、やはり最初はBOXの中央を通る縦の中央線から描いていきましょう。
中央線は関節点を把握するのに非常に役に立ちます。最初にBOXの概形から描き始めたとしても、最終的には中央線を描いて関節点の位置を求めなければなりません。だったら最初から描いたほうが無駄がありません。
まず縦の中央線を描きます。そしてその中心位置もチェックしておきます。
画像:頭部BOXの縦中央線とその中心位置。
そして縦の中央線だけでなく、横方向の中央線も、2方向描いておきます。この2つの中央線は、最終的に描画する各辺の長さを示しています。どういうことかというと、
画像:3方向の中央線と、BOXのすべての輪郭。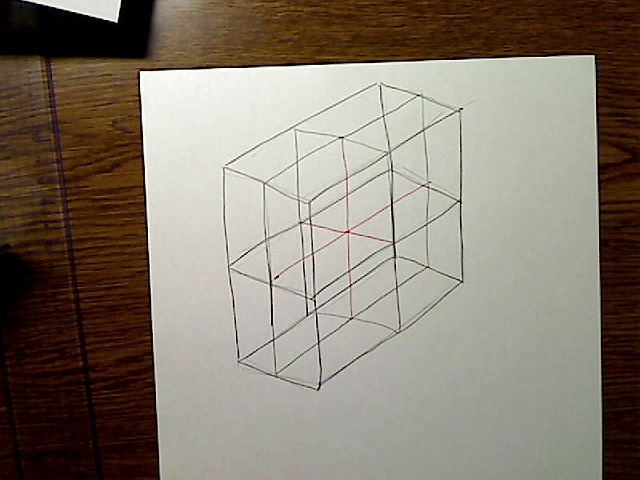
このように、BOXの縦、横、奥行きの3方向について、合計3本の中央線を描きます。
これら中央線の長さは、最初に求めた各辺の長さと同じです。
画像:中央点から引いた3本の方向の中央線は最終状態の各辺の長さを示す。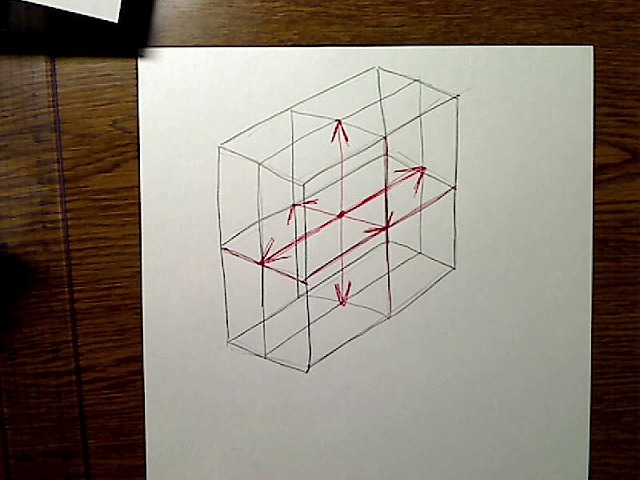
この新しい2本の中央線は、最初に計算で横と縦の長さ(X座標とY座標)を出しておきました。
画像:中央2本線の横の長さと縦の長さ。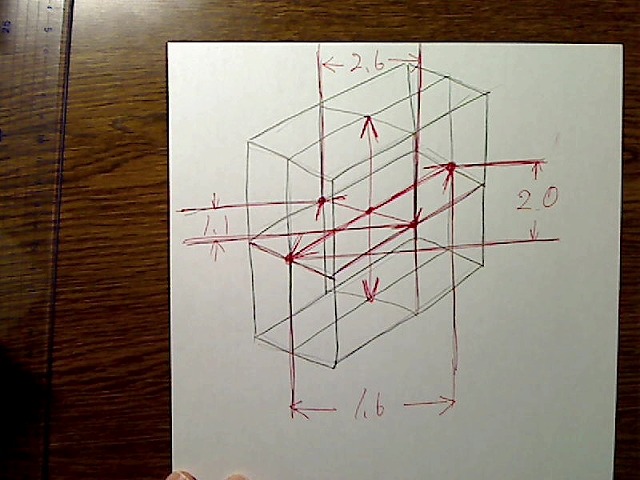
このように、どの部分がどの長さを簡単に示した設計図を作っておくと、後で間違わずにすみます。
これらを参考に、合計3本の中央線を描きます。
画像:3本の中央線。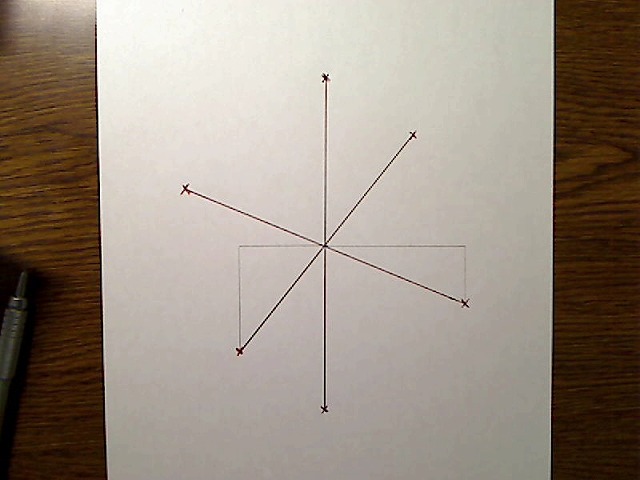
後はBOXの輪郭線を描くだけです。輪郭線の各辺の角度は、この3本の中央線と平行になります。それぞれへ移行方向に描き、BOXの角はそれらの交点になります。
画像:BOXの輪郭を描画。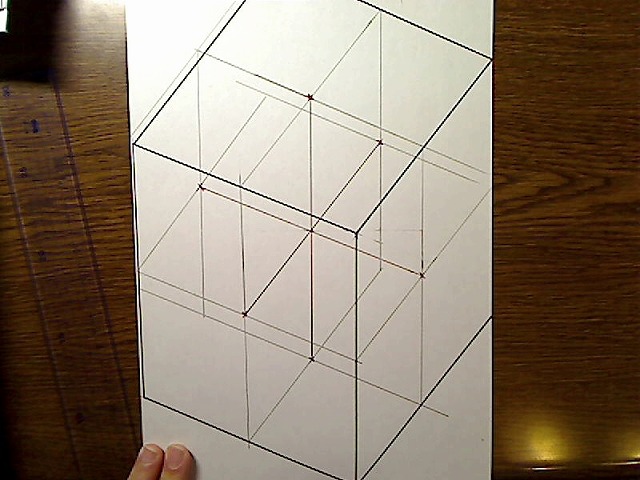
このような順でBOXを描いていきます。関節点はほとんどのBOXで中央線上かその付近にあるので、中央線の位置を参考にしながら次のBOXを描いていきます。
今回は顔面のパーツも描いていきます。顔面パーツ(目、鼻、口)の位置については、前の章を参考にしてください。
画像:顔面パーツと髪。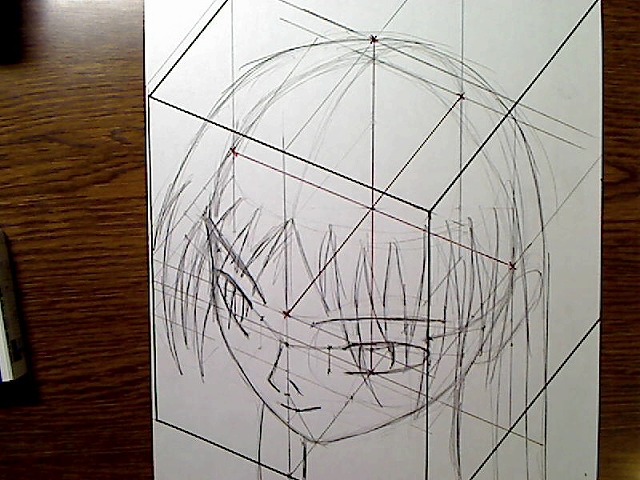
ところで、今回は45度も下方向に回転させてしまったので、顔面パーツが見えにくくなっています。
眉毛や目が釣り上がって見えますが、このキャラクターは実際は目は釣り上がっていません。
しかし実際のところ、かなり上から見ると、どんな人でも目が釣り上がって見えるものです。逆に下方向から顔を見ると、垂れ目に見えます。
画像:3DCGで補助線を見た図。上45度と下45度。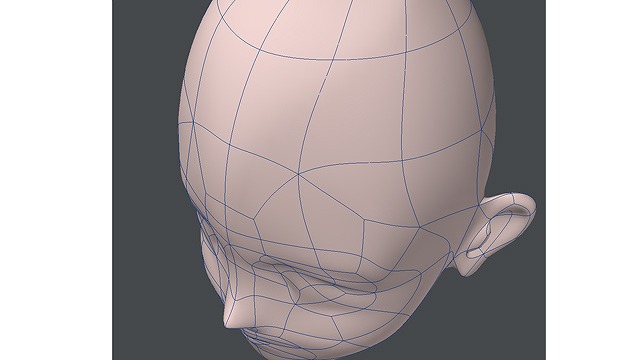
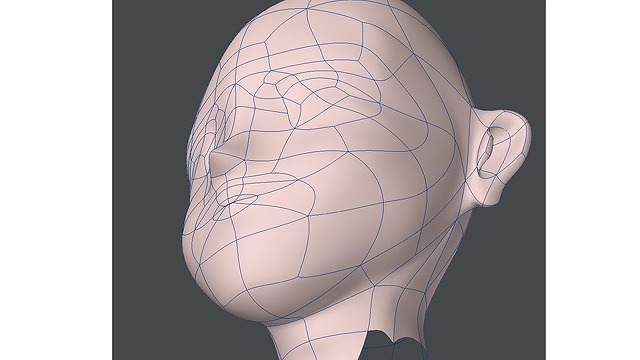
この描き方は3次元的に矛盾なく描いているため、現実の見え方をそのまま再現してしまいます。マンガやアニメ的な描きかたでは、こういった問題を修正して描画することが多いので、こういった描き方をすると不自然に見えるかもしれません。
立体的な位置関係は間違ってはいないので、線の曲率などを少し修正したほうが、キャラクターの描画としては自然に見えるでしょう。