遠近法の拡大縮小具合
さてこれでBOXはどんな角度からでも描けるようになったと思われるかもしれませんが、最後の問題がまだ残っています。
それは「遠近の拡大縮小」の問題です。何かというと、数学的な値は三角関数で求められるのですが、実際にはカメラからの距離によって、物体は大きく見えたり小さく見えたりするのです。
遠くのものほど小さく見え、近くのものほど大きく見えます。三角関数で計算しただけでは、これら大きさの問題は考慮されていません。
もう少し突っ込んで考えてみましょう。たとえば目の前に1本の横の線があったとします。これの長さを100としましょう。
画像:真横の線、長さ100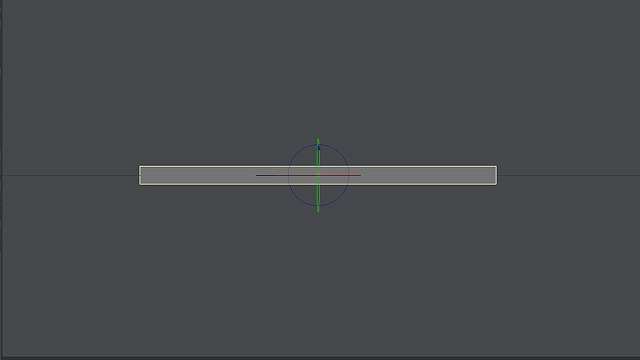
これを横へ奥行き回転で30度回転させるとします。その回転の中心はこの線の中心だとしましょう。
画像:30度回転させた図。左半分のほうが計算値より少し長く、右半分は計算値より少し短い。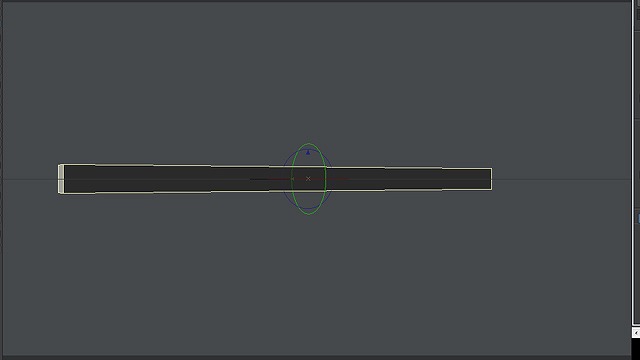
30度回転させるとcos30度で0.85倍になるはずです。しかしそれの長さの計算は「回転前のカメラと物体との距離=回転後のカメラと物体との距離」であると仮定したときの長さです。
回転後、図の場合、線の中心よりも左側はこちら(カメラ)へ向かってきており、線の中心よりも右側は奥側へ遠のいています。
なので、中心より左側は計算した値よりも少し長く、中心より右側は計算した値よりも少し短くなるのです。
要するに、BOXを回転させたときは、奥側はBOXそのものが小さくなり、こちら側はBOXそのものが大きく見えます。極端なカメラの設定でそれを見てみます。
画像:BOXを回転後、こちら側が大きく見える図。極端な図。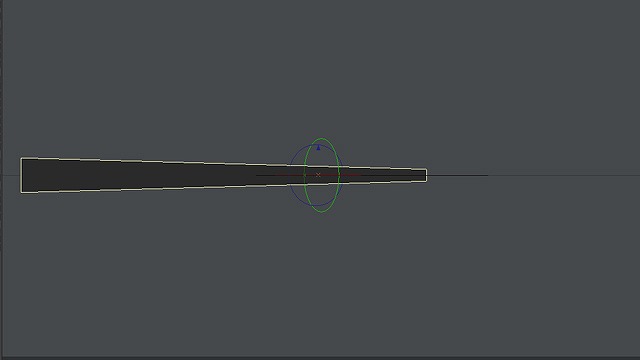
実はこうした問題は、頭部を描く際にはほとんど気になりませんでした。
こういう奥行き距離による拡大縮小問題は、奥行き方向へ細長いものほどより大きく出てきます。頭部のように、全体的にあまり細長くない形については、あまり気にならなかったのです。
しかしたとえば、腕や脚のような細長い部分を奥行き方向へめいいっぱい突き出した場合、拡大縮小をまったく考えない絵を描いてしまうと、まるで腕が単に短くなったように見えてしまいます。
画像:拡大縮小のない、腕をこちらへ突き出している図。腕が短く見える。
腕がこちらへ向かうにつれ、BOX全体を大きくしなければなりません。
画像:拡大縮小を込めた、腕をこちらへ突き出した図。自然に見える。
それではこれらの「拡大縮小具合」は、どれくらいの数値にすればいいのでしょうか?
適当な値で拡大縮小
この拡大縮小の具合については、実は適当な値でもかまいません。
腕のBOXをこちらへ向けて描いてみます。先ほどと同じく、胴体から上腕と下腕をこちらへ伸ばして突き出しているようなポーズを仮定しましょう。
このとき、胴体はふつうのBOXの数値計算で出した値です。胴体とカメラの距離でこの値です。
すると上腕の付け根部分でのカメラとの距離は、胴体とカメラの距離と同じなので、拡大縮小はこのままでかまいません。となると、腕はこちらへ向かってくるにつれて、計算値よりも大きくなってこなければなりません。
まず上腕のこちら側の面です。この面を大きくします。どれくらい大きくするかは、後で説明しますがカンでかまいません。ここでは1.2倍とします。
このとき、こちら側に向かってくる線についても1.2倍します。
画像:上腕のこちら側の面を大きくする図。1.2倍する。こちらに向かってくる線も1.2倍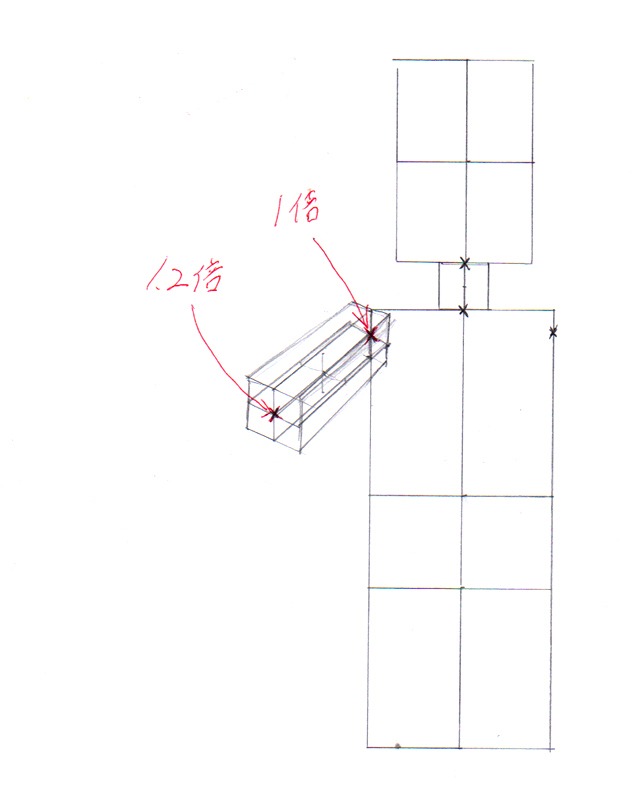
このように、こちら側の四角の面を大きくしてBOXの輪郭線を描きます。後はこれに従って輪郭線を描いていくだけです。
下腕もこのようにして、こちら側の面を1.2倍します。
ただ、下腕は付け根の面の部分ですでに1.2倍になっていますので、手首の辺りだと1.2倍の1.2倍なので、1.44倍になります。およそ1.4倍としましょう。
画像:上腕の付け根は計算値の1.2倍、手首辺りは1.4倍と計算。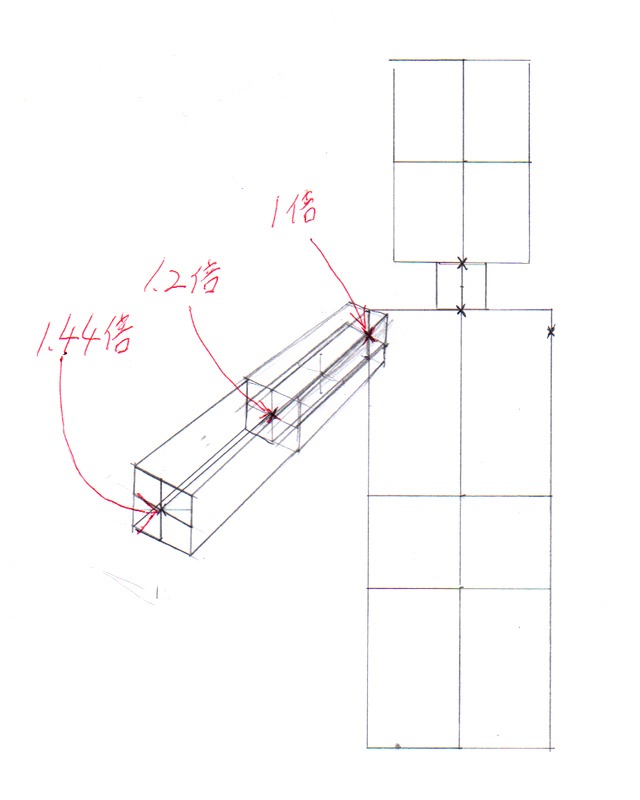
このように、BOXのある面の大きさを描くのに、カメラとの距離によって何倍かして描画します。
この倍率は、通常は1.05〜1.2倍くらいに見えることが多いのですが、もっと大きなあるいは小さな数値でもかまいません。
ただし注意点として、倍率が体の部分によって大きく異なる、ということになるとおかしな絵になってしまいます。
たとえば上の図で、上腕の付け根より先端までに1.2倍大きくしましたが、同じくらいカメラに近づくのに、下腕の付け根から手首の辺りまでの倍率が2倍になるとか、こういうことはしてはいけません。下腕の付け根から手首までは、やはり1.2倍くらいの拡大率でないと、下腕だけ突然こちらに急激に迫ってくるような絵に見えてしまいます。
ところでこの「拡大率」には何か法則があるのでしょうか?