カメラの距離
先ほど説明した「物体の遠近によって拡大したり縮小したりする現象」についてですが、これについてもう少し見ていきましょう。
実はこの「拡大縮小率」というのが、物体と目の距離によって変化します。
何かといいますと、たとえば目の前に何か箱型のものがあるとします。
これにめいいっぱい顔を近づけて見ると、こんなふうに見えます。
画像:3DCGで至近距離から箱を見た図(カメラが至近距離)。箱は画面いっぱい
今度は箱からずっと遠い距離から見てみます。するとこんなふうに見えます。
画像:3DCGで遠距離から箱を見た図(カメラが遠距離)
このままでは小さくて見えにくいので、箱を拡大してみます。
画像:箱を拡大。
このように、物体は至近距離で見るほど遠近での拡大縮小率が大きくなります。
反対に、ずっと遠距離から物体を見ると、拡大縮小率が非常に小さくなっていきます。あまりに距離が遠いと、拡大縮小率はほぼなくなります。
今まで三角関数で「見た目の値」を出してきましたが、これらは拡大縮小がゼロのときの理論値です。つまりこれら計算値は、ものすごく遠い距離からその物体を見たときの見え方なのです。
この拡大縮小率はカメラの位置によって変化するため、どんな拡大縮小率を使っても「間違いである」というようなことはありません。だから「拡大縮小率は適当でもいい」のです。
ただし一つの絵の中で、部分によって拡大縮小率が異なると、たとえば手と足で拡大縮小率が異なると、手と足でそれぞれ別の距離から見ているような感じになってしまうので、これは「間違い」になります。
画面の枠
次に画面の枠についてです。
先ほどカメラと物体との距離によって、遠近の付き具合(遠近の拡大縮小率)が変化するといいました。
絵を書くときでも写真を取るときでも、画面には「枠」があります。この枠は現実に目に見えるわけではありませんが、私たちは絵を描くときには適当に枠を取って絵を描いています。
通常はカメラでも肉眼でも、遠距離から見るほど物体は小さく見え、その分上下左右にたくさんのものが見えます。この場合「枠」が大きい状態です。
画像:背景に対して枠が大きい状態
これに対し、もっと物体に接近すると枠が小さい状態になります。
画像:背景に対して枠が小さい状態
遠距離状態で、枠が大きいときと枠が小さいときを比較してみます。
画像:遠距離で、枠が大きいものと小さいもの
さて先ほど説明した、二つの拡大縮小率の異なる箱を持ってきて比較してみます。
画像:拡大縮小率の異なる二つの箱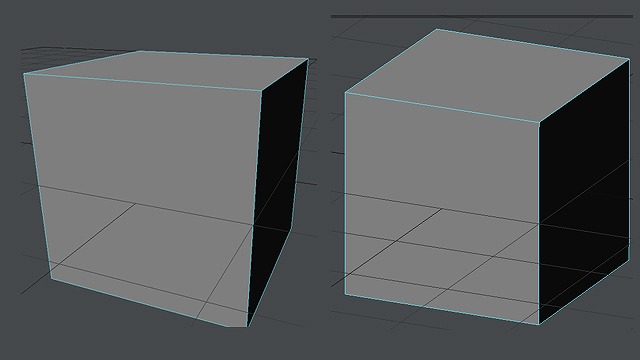
この箱は同じ物体ですが、拡大縮小率の大きい箱のほうは、至近距離で見た図です。
拡大縮小率の低いほうは、遠距離から見た図です。
通常は遠距離から見た場合、物体はとても小さく見えるはずです。この箱も、おそらくふつうはもっと小さく見えるでしょうが、画面の「枠」を小さく取ることで、このように画面いっぱいに箱が見えている、という状態です。
ズームと枠の大きさ
拡大縮小率が小さい、あるいはほとんど付いていないということは、非常に遠くから見ている状態と同じなのです。
実際に絵を描くとき、画面の枠いっぱいに小さな物体を描くと、非常に近くから見ているように感じます。それにも関わらず、拡大縮小率を小さく描いてしまうと「すごく遠くから見ているのに小さい物体が画面いっぱいに見える」という状態で、現実味がないと思われるかもしれません。
しかしこのような写し方は、昔は不可能でしたが現代では可能で、私たちは案外慣れています。たとえば遠距離から写真を写し、できた画像の一部を切り取って拡大したような感じです。
あるいはビデオカメラなどで、遠距離からめいいっぱいズームさせたような状態です。
なので実際のところ、この拡大縮小率は「適当」でもおかしな絵には見えたりはしません。
ただ、
手前と奥の拡大縮小率を大きくすると至近距離から見ている状態
手前と奥の拡大縮小率を小さくすると遠距離から見ている状態
であることは覚えておきましょう。
それは表現のしかたにも影響してきます。たとえば何かが目の前に接近してくるようなとき、この拡大縮小率を大きくすると、まるで至近距離でそれを見ているような表現になり、迫力が増します。
逆に写真で顔を写すとき、顔の至近距離からカメラで写してしまうと、拡大縮小率が大きくなるため、レンズの近くにある鼻や口が妙に大きく見えてしまい、顔がきれいに写りません。
また3DCGにおいては、この枠の大きさは「ズームファクター」などという数値で表されます。文字通りビデオカメラなどで使うズームの値のことで、これを変化させると物体はより大きく見え、枠は狭くなります。
しかしあくまでズームしているだけで、物体とカメラの距離が変化するわけではありません。だからズーム値を変化させても、 物体の手前と奥の拡大縮小率は変わりません。
ズームファクター(ズーム値)は枠の大きさを変えるだけであり、カメラとの距離(拡大縮小率)を変えるものではありません。
「無限遠方」とは?
三角関数で求めた値は、この拡大縮小率がゼロの状態の値、いわばものすごく遠い距離から物体を見た状態と同じです。
ではその「ものすごく遠い距離」はいったい何メートルのことでしょうか?
実はこの拡大縮小率は、人間の目で見ている限り、どんなに遠い距離から見てもほんの少しはついています。
1キロ先だろうが100キロ先だろうが、やはりほんの少しだけ拡大縮小はついています。
拡大縮小率がゼロになる距離というのは現実には存在しないのですが、仮に「無限に遠い距離」から見た場合はゼロになるだろう、というような意味で、この無限に遠い距離のことを「無限遠方」と呼びます。
厳密には無限という距離は存在しないので、「限りなく無限に近づけたときに限りなくゼロに近づいていく」という、ややこしい定義をしますが、わかりにくければ要するに
とてつもなく遠い距離から見たら拡大縮小率はゼロになる
と覚えておいてもいいでしょう。
別に数学的に厳密な定義はどうでもいいのです。私たちの目的は絵を描くことなのですから。
平行カメラ
またこのように、拡大縮小率がゼロになるような写し方をするカメラのことを「平行カメラ」といいます。
箱型の物体など、こちらに向かってくる線が完全に平行になるためにそのように呼ばれるのでしょう。
しかし現実世界では必ず遠近による拡大縮小は発生するので、平行カメラというのは現実には存在しません。
これは設計やCGなどで、特殊な用途で用いられる仮想のカメラです。たとえば家の設計図や部屋の間取り図は、真上や真横から見た図で、手前と遠方の拡大縮小はありません。