市販の遠近法理論でよく使われる図法に「透視図法」というのがあります。復習の意味でもこれの説明をしておきましょう。
透視図法には「一点透視図法」「二点透視図法」「三点透視図法」などあります。
消失点とは?
透視図法をやる前に「消失点」というものについて簡単に説明しておきます。
画面の中で、ある地点から奥行き方向へずーっと線を伸ばしていくと、ある一点へ向かうようになります。この点を「消失点(Vanishing Point(バニシングポイント)」と呼びます。
いわば「奥行き方向へ無限に伸ばしたところ、行き着く先の一点」といったところです。
重要なこととして、ある物体のある線の消失点がわかっていても、その「線の角度」がわかるというだけで、「線の長さ」まではわかりません。
消失点の位置が正確にわかれば、消失点へ向かって線を引けば、それで線の「正しい方向」は描けるのですが、「線の長さ」まではわからないということです。しかし線の長さについては、すでに三角関数でおよその値を出す方法を学びました。
これからやるべきことは、三角関数で出した線の長さを、消失点などの理論を使って「どれくらい遠近で拡大縮小させるか」を学ぶことです。
一点透視図法
一点透視図法というのは、消失点が一つしかない図形のことです。たとえばこのような図です。
画像:3DCGで箱が3つある。一点透視図法の図。奥行きの線を色を変える。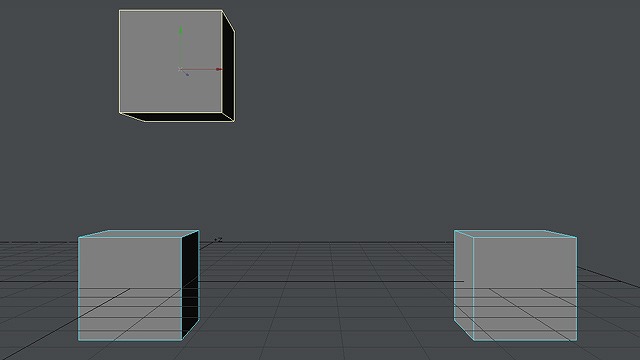
図の奥行きへ向かっている線は、すべて同じ一点を目指しています。
画像:奥行き線がすべて一点を目指している図。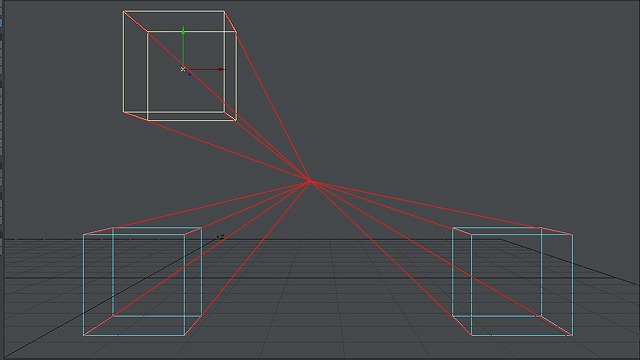
このように、奥行きへの線が一点の消失点に向かっている図法を一点透視図法と呼びます。
ここで一つ重要なことはこれら奥行きへ向かっている線、いわば「消失点へ向かっている線」は、すべて平行であるということです。
平行であるということは、たとえば真上から見ると、すべて平行になっているような状態です。
画像:真上から平行カメラで見た図。一点透視図法。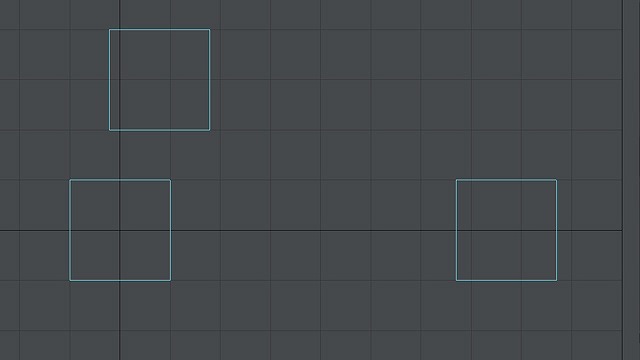
一つの消失点に向かうすべての線は、すべて平行、いわば同じ角度で並んだ状態です。これは重要なことなのでよく覚えておいてください。
二点透視図法
次に二点透視図法を見てみましょう。これは消失点が二つあります。
画像:3DCGで箱が3つ、二点透視図法。
奥行きへ向かっている線は、消失点である2つの点のいずれかを目指しています。
画像:奥行き線が2点を目指している図。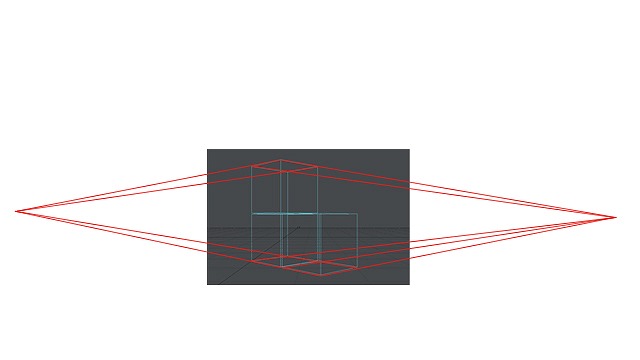
消失点(奥行きの線が向かう方向の行き着く限界先)が2つあるので「二点透視図法」と呼びます。
ここでもやはり、「同じ消失点へ向かっている線はすべて平行」です。
画像:真上から平行カメラで見た図。二点透視図法。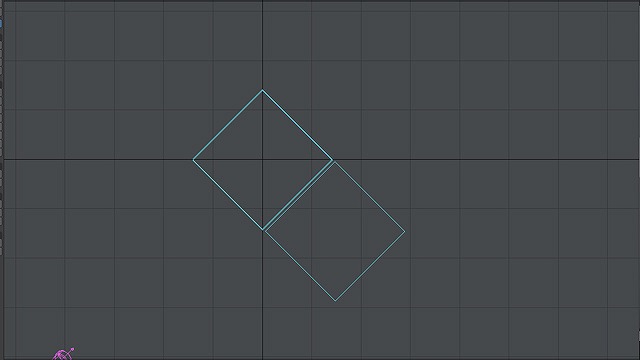
三点透視図法
二点があるなら三点もあります。三点透視図法では消失点が3つ、左右と上にあります。
画像:3DCGで箱が三つ。三点透視図法。
奥行きへ向かう線は、すべて消失点の3点のどれかに向かっています。
そしてここでもやはり、同じ消失点へ向かう線はすべて平行、つまり「同じ角度」です。
複数点透視図法
さてここまで、美術の本でよくある典型的な透視図法の説明をしてきました。
これらの中で最も重要な法則は
同じ消失点へ向かう奥行き線はすべて平行である。同じ角度である。
ということです。
これについて落ち着いて考えてみるとわかるのですが、このやり方では、奥行き線については、1〜3つの角度のものしか描けないのです。
たとえば一点透視図法では、奥へ向かう線はその消失点へ向かう角度のものしか描けません。
これはつまり、奥へ向かう線はすべて平行でなければ、この図法は使えない、ということになります。
画像:一点透視図法の絵。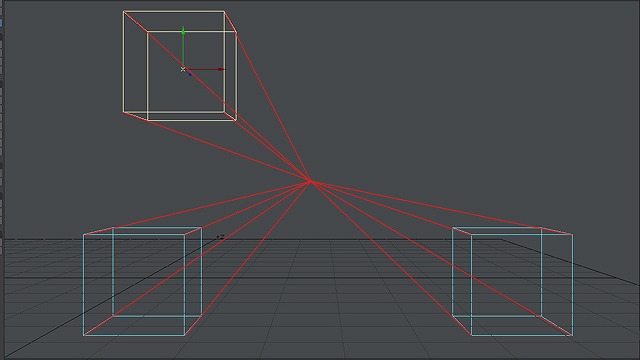
幸いこの図形では、奥行き線はすべて完全に平行なために絵として成立していますが、少しずれていたらどうなるでしょうか?
画像:一点透視図法の箱の一つを少し角度をずらして消失点を変える。ずらした箱の奥行き線は別の消失点へ向かう。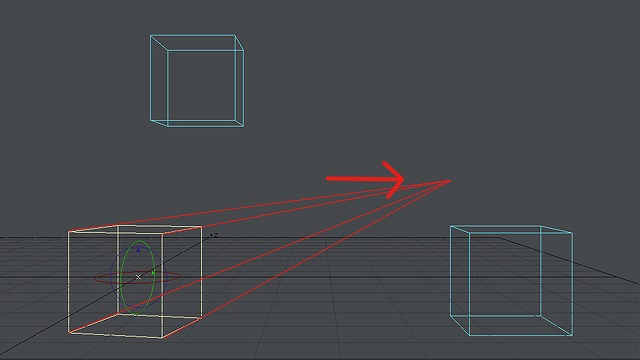
このように消失点はずれてしまい、ずれた箱の奥行き線は別の消失点へ向かいます。
ほかの箱も少し回してみましょう。
画像:すべての箱の回転角度を変え、消失点がばらばらになるようにした。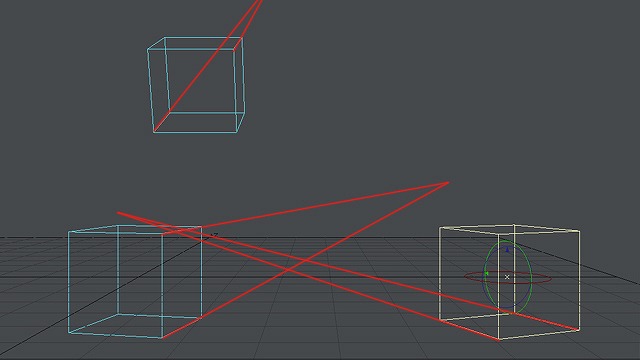
すべての箱をでたらめに回転させたので、消失点が一つでなくなり、たくさん出来上がってしまいました。
これでは一点透視図法も三点透視図法も使えません。
もっと極端な例を出してみましょう。
画像:無数の箱がでたらめに回転している絵。
このような回転になってしまうと、消失点は無数にできてしまい、透視図法もまったく使うことができません。
透視図法の限界
実はいうと、この透視図法というのは「奥行き線がすべて平行(同じ角度)の物体にしか使えない」のです。
しかし現実に、完全に平行な線というのはめったに存在しません。建築物でさえ、完全に平行に規則正しく並んでいるものはほとんどありません。
たいていは、どんなに規則正しく並べようとしても、少し外れたりするものです。
このような透視図法は厳密な模写図にはあまり使えず、たとえば原子の格子図のような、特殊な図でしか使えないのです。
あるいは、よほど規則正しく並んでいるビルや、建築物の間取り図などを描きたい場合は、使えるかもしれません。
特に建築物の内部では、非常に正確に規則正しく柱などを配置しないと危険なこともありますので、こういう場合は消失点を取って計算して描いてもいいかもしれません。
それでもたとえば並んでいる本や箱などを描くとき、消失点を取ってそれに沿って描いてしまうと、不気味なくらい規則正しく並んでしまい、不自然に見えてしまいます。
人間が作った多くのものでは、完全に規則正しく並んでいるものはあまりありません。
では透視図法というのは、使えるようで使えないものなのでしょうか?
消失点の正体
その前にまず、消失点というのが何者なのか、はっきりさせてしまいましょう。
先ほどから「消失点が同じ奥行き線は、すべて同じ角度であり、平行である」といってきました。
三点透視図法では消失点が3つありました。だからこの図法での奥行き線は、3つの角度しか表現できなかったのです。
逆にいうと「奥行き角度の違う線は、すべて異なる消失点に向かう」ということでもあります。
もう少しいうと「奥行き角度によって消失点がそれぞれ存在する」という意味です。
出だしの位置は?
消失点は奥行きの角度によってだけ決まるのでしょうか?線の出だしの位置によっては変わらないでしょうか?
ちょっと3DCGを使って実験してみましょう。
「線の出だしは違うけど、見た目の角度(奥行きの角度)が異なるいくつかの線」を用意します。
画像:出だしが異なるが同じ角度の線を3本。消失点が同じ。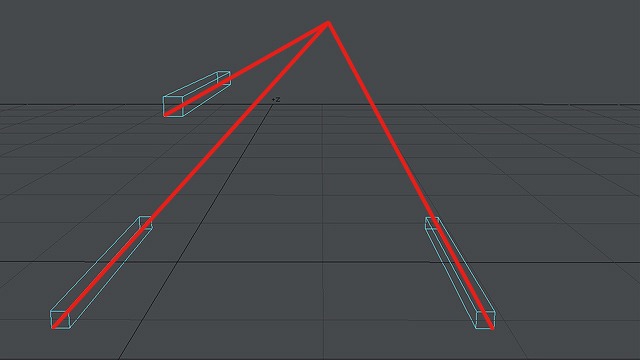
このように、消失点は同じ位置になります。どうやら出だしの位置は関係なく、角度によってのみ消失点は決まるようです。
もう少し実験してみましょう。今度は出だしが同じ位置で、異なる奥行き角度に向かわせてみます。
画像:出だしが同じ位置で、奥行き角度が異なる3本。消失点が異なる。
出だしの位置が同じでも、奥行き角度が異なると消失点は異なります。やはり消失点は、出だしの位置に関係なく「見た目の角度」によってのみ決まるようです。
消失点と無限遠方
消失点は、なぜ出だしが異なるのに同じ位置に行き着くのでしょうか?
そもそも「消失点」という一点に集まるからには、「ずっと先へ伸ばすとほぼ同じ位置に来る」という意味のはずです。
たとえば3メートル離した出だしの位置から、同じ角度で奥へ線を伸ばしてみます。
画像:3メートル離した出だしから同じ角度へ奥へ向かう。
このときずっと奥のほうではどうなっているでしょうか?
ためしにカメラを1000メートル先へ移動させてみてみると、やはりこの2つの線は3メートル離れたまま平行でずっと先まで続いています。
画像:1000メートル先の2つの線
しかし元の場所から見ると、1000メートル先の「3メートル離れた線」など、くっついているも同然です。だから同じ位置に見える、つまり一つの消失点に行き着くのです。
一つの消失点に行き着いても、厳密には少しだけ離れています。
これがたとえば、3メートル離れているのではなく、1万メートル離れている2本の線であれば、遠く奥へ向かってもまだけっこう離れているように見えるでしょう。もっとも現実には、元の位置で出だしの位置が横に1万メートルも離れた奥行き線など画面に入りきらないので描くことはできませんが。
それでは「出だしの位置は同じだが角度が異なる2つの線」はどうでしょうか。
画像:出だしは同じだが角度が少し異なる2線。原点。
この2つの線を、奥へ1000メートル行った場所で、どうなっているか見てみましょう。すると……
画像:1000メートル先。
このように、2つの線ははるか遠くに離れてしまいます。出だしの角度が違ったのだから、奥へ行くにつれてどんどん離れてこうなったのです。もう一方の線は、遠すぎてどこにあるのかよくわかりません。
元の位置から見ると、この2線は異なる消失点に行き着いています。ずっと遠くでは、ずっと離れています。
消失点群という概念
ここまで「奥行きの線」というものについて見てきました。
奥行き線の向かう先である「消失点」は、実は「角度によってのみ決まる」ようです。線の出だしの位置には関係がありません。
さて「見た目の角度」というのはどういうものでしょうか?
たとえば自分が直立し、真正面を見ているとします。このときの焦点を0度としましょう。
画像:画面の左右0度の点を取る。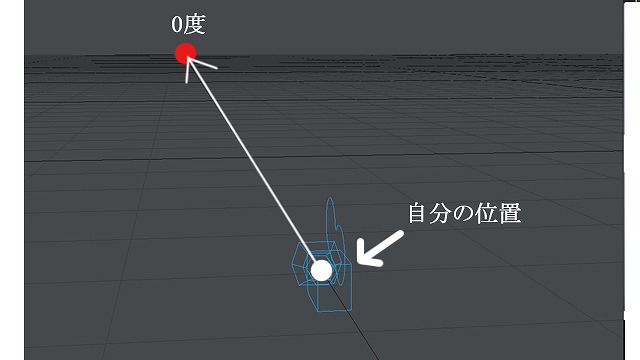
この点を0度とします。ここへ向かう線は、要するに自分から見てまっすぐ前の線です。
これを試しに15度右へ回転させて見ましょう。すると奥行き角度が変わり、右15度の消失点へ向かいます。
画像:右15度の消失点へ向かう線を追加。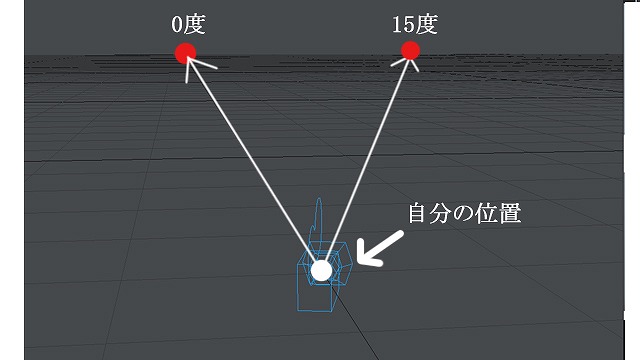
もう少し回転させ、今度は右30度へ向かう奥行き線を描いてみます。
画像:右30度へ向かう奥行き線。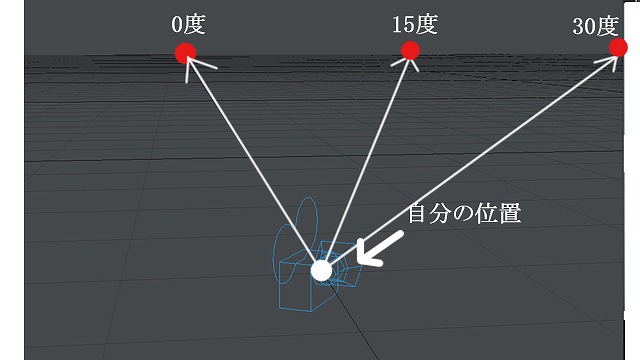
見た目の角度によって、それぞれ消失点があります。これを15度おきに描いてみると、およそこんな感じになるでしょう。
画像:15度おきに描いた右方向への消失点。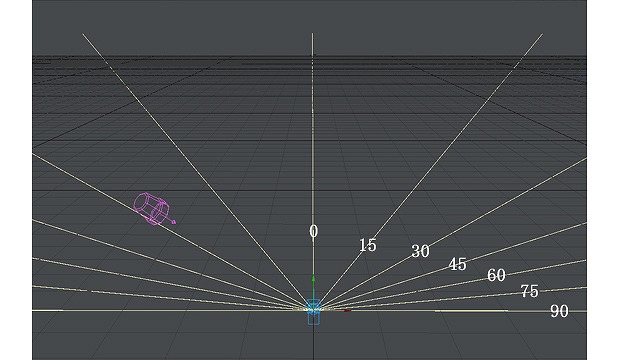
これは左方向でも同じです。左も同様に描いてみます。
画像:左方向へも消失点。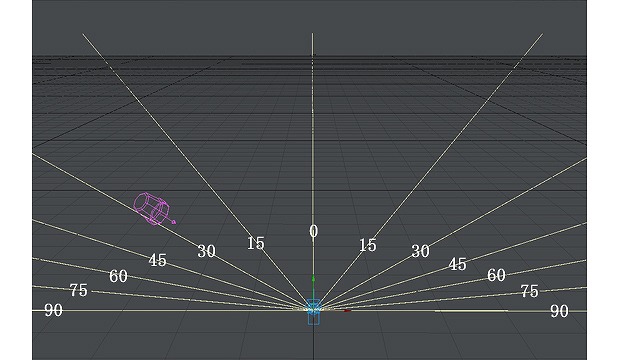
さて、今左右へ向かって消失点を描きましたが、当然上下方向にも同じことがいえるはずです。
上下方向にも同じように描いてみます。
画像:上下方向へも消失点。
奥行き方向といっても、上下左右があります。先ほど「右へ15度の消失点」とかいいましたが、同じように右へ15度奥行き方向へ向かっても、上下の角度が異なると別の消失点に行き着きます。
たとえば「右へ15度上下は0度」の消失点と「右へ15度上へ30度」の消失点は、異なる位置になります。
画像:右15上下0度の消失点と、右15度上30度の消失点へ向かう線。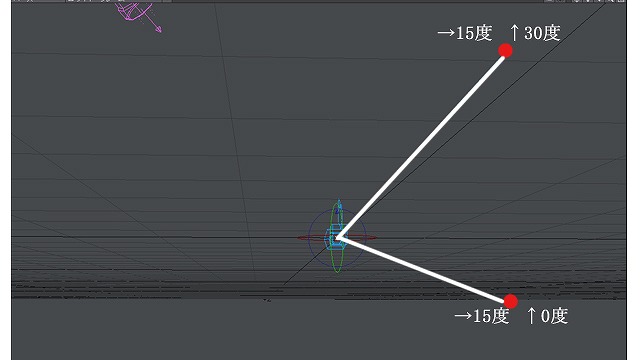
「右15度」の消失点は、どうやら右15度の位置に縦線を引いた、そのいずれかの位置になりそうです。
画像:右15度の消失点を通る縦線。15度の消失点群。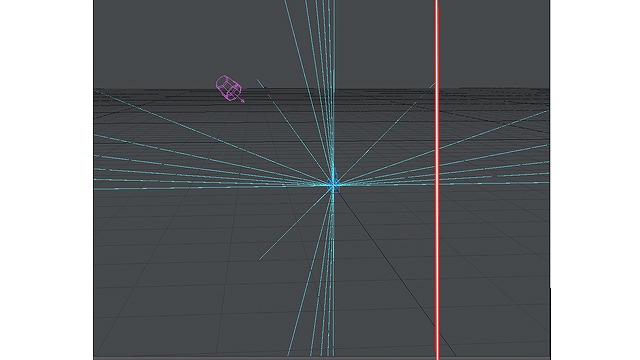
右15度でも、上下方向によって消失点が異なりますので、このように右15度に縦線を引き、これを「右15度の消失点群」と呼ぶことにしましょう。
このようにして、それぞれ消失点群を線で描いていくと、こんなふうになります。
画像:消失点群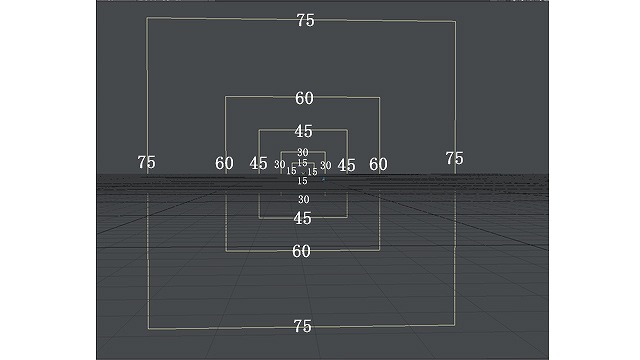
このように、たとえば右15度の消失点上の縦線は「右15度の消失点群」上30度を通る横線は「上30度の消失点群」となります。
これら消失点群は、まるで網の目のような形としています。網の形をしているので、これらを「消失点群」と呼ぶことにしましょう。
この「消失点群」の概念を理解していると便利です。
たとえば「右へ15度、上に15度へ向かう奥行き線」の消失点の位置はどこになるでしょうか?
もちろん、右15度の縦線と、上15度の横線の交わる位置が消失点になります。
このように、横角度と縦角度を定めれば、後は消失点群の指定の点を取れば、奥行き線の角度はわかるわけです。
そして奥行き線の長さについては、三角関数で出せばいいのです。これで奥行き線について、「方向」と「長さ」も両方わかったので、後は定規で線を引くだけです。
最初に画面に消失点群を描いてしまえば、後は角度を設定すれば線が引けます。
消失点群の正確な出し方
さて、先ほどは適当に消失点群を描いてしまいましたが、これらの線は正確な位置に描かないと当然、正確な絵にはなりません。
これら消失点群の線の位置は、正確に数字で出す方法はあるでしょうか?
答えはもちろんあります。ただ説明は、またもや数学的なもので、けっこうややこしいものになります。
しかし理屈はともかく、絵を描くときには消失点群の正確な線の位置が描ければそれでいいのです。
理屈がよく理解できなければ、とりあえず描き方だけ覚えてください。また数字で覚えるのが面倒だという方は、「だいたいこれくらいの位置関係になる」ということをイメージで覚えてしまいましょう。
これら消失点群というのは、要するに消失点がどこにあるか、という指標を示すものです。建築物などを描く場合は重要になることが多いです。
数字でなくても「およそこのへん」というカンだけでも身につけておくと便利です。
では次から、消失点群の線の正確な位置を、計算で求めていきます。