ここまで遠近法について延々と説明してきました。これで建築物などの奥行き線の角度については正確に描けるようになりました。
ではBOX理論にどうやって応用するのでしょうか?
この章の最初のほうで、BOXの面の拡大縮小についてお話しました。この拡大縮小率については、とりあえず「適当に」といっていました。
画像:BOXの奥と前面の拡大縮小。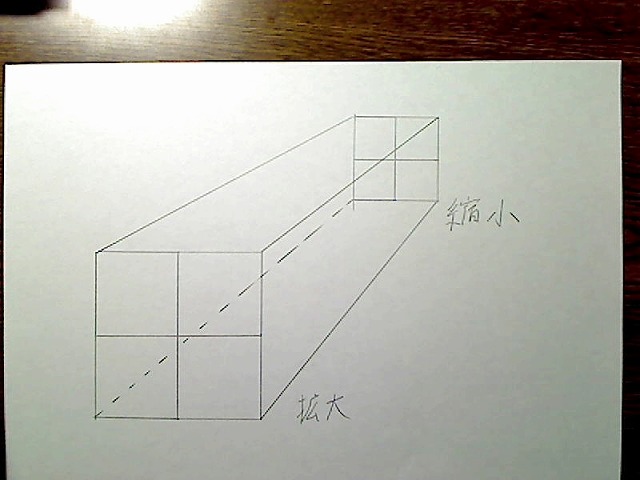
この比率をもう少し正確に出してみます。
ただ最初のほうでもいっていますが。この計算方法はかなりややこしいので、毎回あまり厳密に計算するのはかなり面倒です。
それでも慣れるとすぐに計算できるようになってきますが、あまり敷居を高くするとやりにくくなってきます。
またカメラと物体のとの距離によって拡大縮小率も変化するので、結局は「適当に拡大縮小」というやり方でも十分まともな絵になります。
ここからはとりあえず計算していきますが、無理に理解しようとする必要はありません。知っていると便利かもしれない、という程度です。
さてここでは「三角形の相似の計算」を使うので、相似計算について復習しておきましょう。
三角形の相似
二つの三角形が「同じ形をしていて大きさだけ違う」という場合、この2つの三角形は相似の関係にあると呼びます。
相似関係にある三角形は、比率計算でお互いの辺の長さを出すことができます。たとえば次の2つの三角形は、形は同じです。
画像:同じ形の(相似関係の)2つの三角形で、大きさは2倍違う。小さいほうの辺の長さは、3,4,5で、大きいほうは6,?,?とする。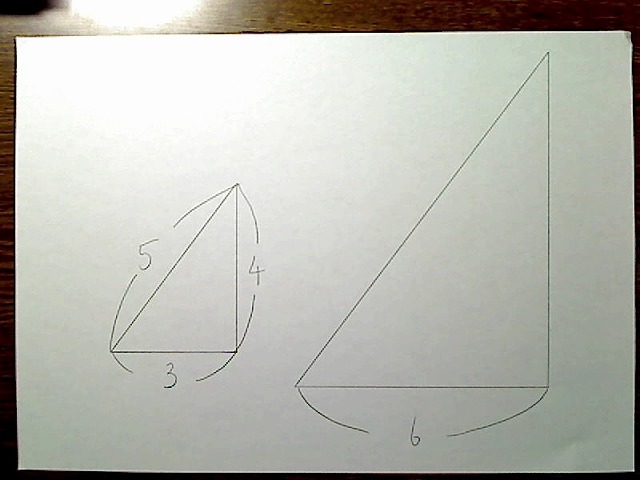
この場合、小さいほうの3センチの辺は、大きいほうでは6センチになっています。だからこの2つの三角形は、大きさが2倍違うということです。
だからほかの辺の長さも2倍違います。大きいほうの三角形の辺の長さは、6,8,10となります。
画像:大きいほうの三角形。辺の長さが6,8,10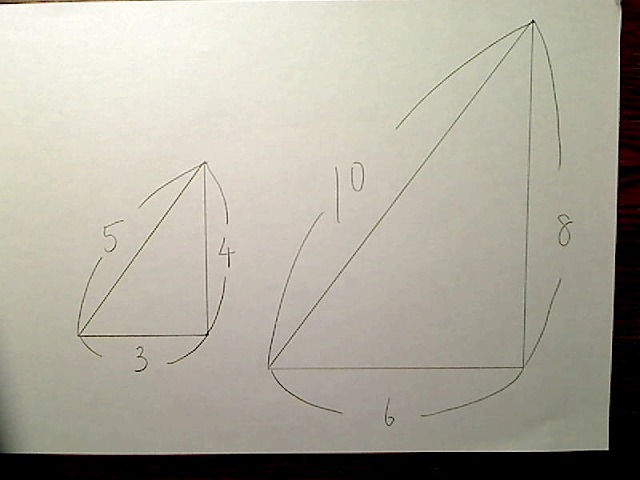
このように、相似関係にある2つの三角形では、その倍率がわかれば、片方の辺の長さがわかればもう片方の線の長さもわかるというわけです。
三角形の相似の条件
2つの三角形が相似関係になる条件は、3つあります。
見ていきましょう。
3組の辺の比がすべて等しい
画像:2つの三角形、辺の比率がすべて2倍。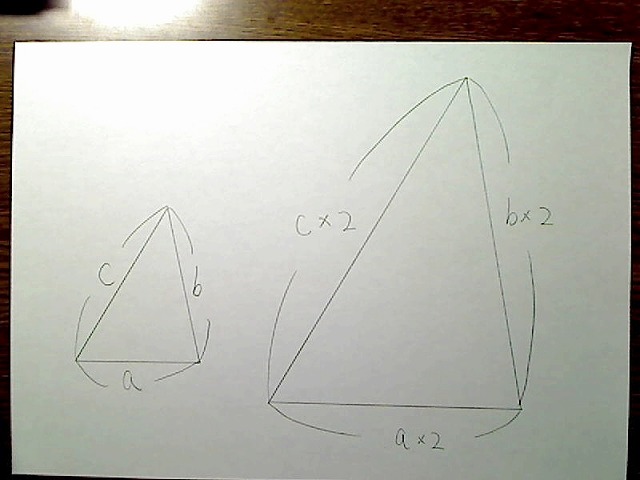
2組の辺の比とその間の角度がそれぞれ等しい
画像:2つの三角形、2辺の比率が2倍で、その間の角度が同じ。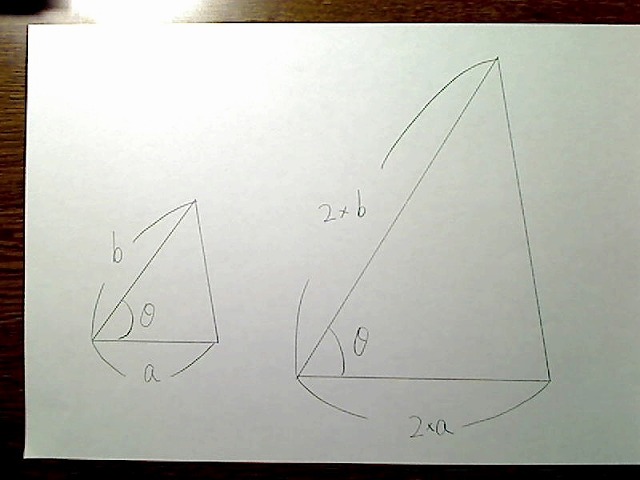
2組の角度が等しい
画像:2組の角度が等しい2つの三角形。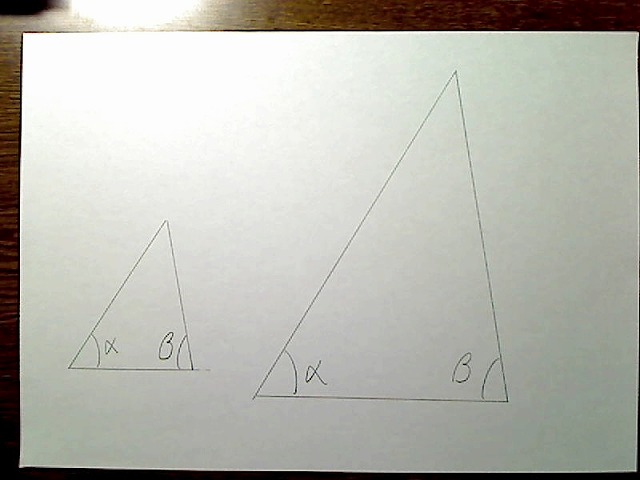
このような条件のときに2つの三角形は相似関係になります。
ところでそれをどう利用するのでしょうか?遠近法で利用するときは、次のような形を想定します。
画像:一つの三角形の中で、中間に1本、線で分けたもの。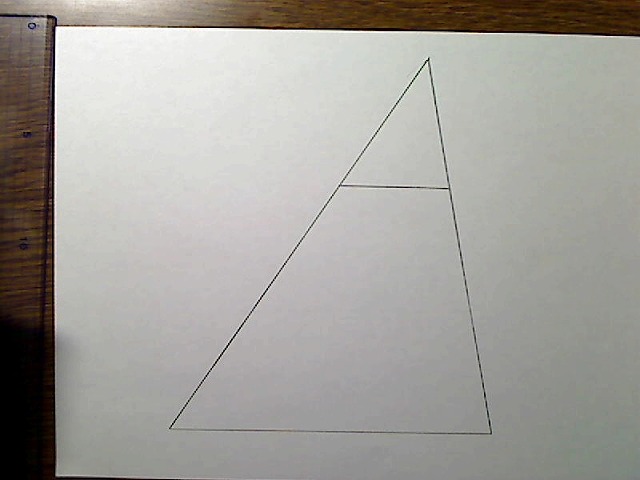
実際ではこのような形を扱います。大きな三角形があり、これを線で分けます。
その分ける線は、図のようにたとえば2つの辺を3分の1の位置でわけるとします。
このとき、大きな三角形の中に小さな三角形が入っているような形になりますが、この2つは相似関係になります。
画像:大きな三角形の中に小さな三角形があり、これらが相似関係にあることを説明。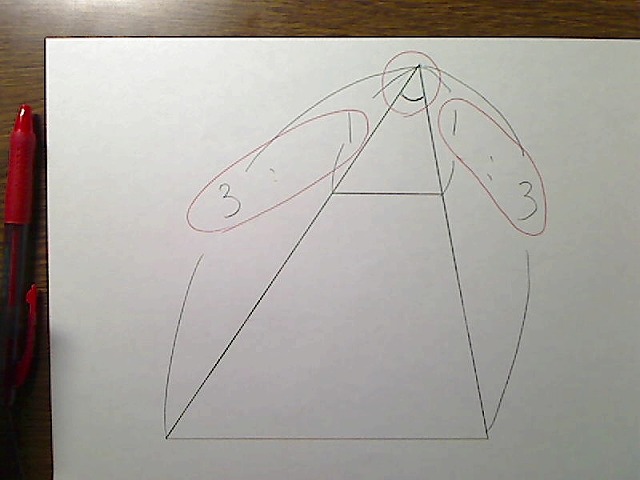
2辺をそれぞれ3分の1でわけているので、この2辺の長さの比は同じです。これに加え、その間の角度は見てのとおり同じです。
なので「2組の辺の比とその間の角度がそれぞれ等しい」という関係になり、相似になるわけです。
たとえばBOXを横に回転させてみて、その奥の面の辺から消失点へ向かって線を引きます。
画像:回転後のBOX(拡大縮小あり)から消失点へ向かって線を引く。相似関係にある2つの三角形を示す。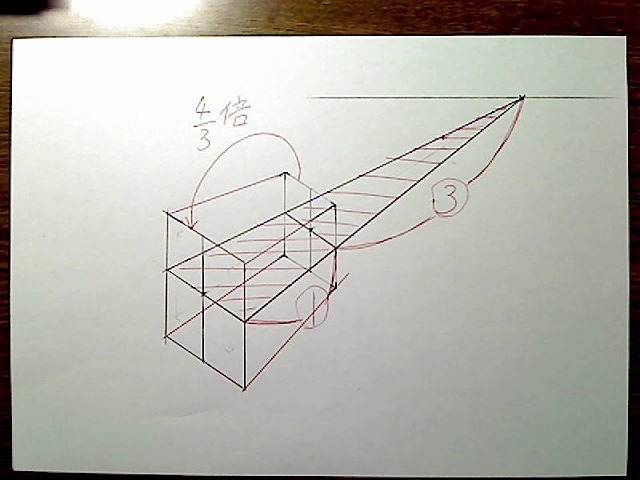
このように2つの三角形が相似関係になります。たとえば奥の辺から消失点までの距離を3とし、BOX奥行き線の長さが1とすると、このようになり、この2つの三角形は3:4になりますので、前の面の四角形の辺の長さは、奥の面の四角形の3分の4倍になります。
このようにして、奥の面の四角形と消失点の距離を測定することで、そこから前面の四角形の倍率を出すことができます。
座標系の問題
さて、この章では遠近法について見てきました。しかし実際に紙に「消失点群」を書いてからBOXを回転させると、不都合な問題が起こります。
たとえばまったく回転させていないBOXが目の前にあるとします。
画像:回転なしのBOX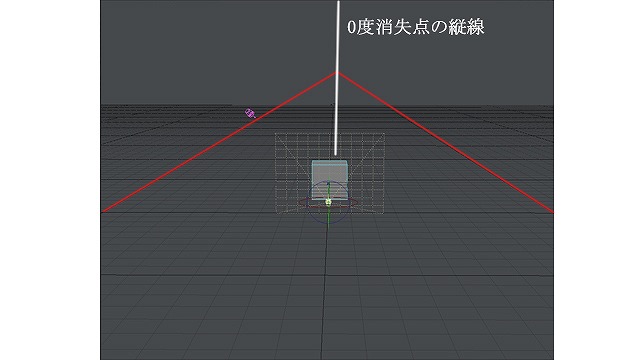
回転させないこのBOXは、きっとこんな形をしているでしょう。このBOXの奥行き辺の延長線上は、消失点群の0度の位置に行き着くはずです。
しかしこのBOXを置く位置によっては、0度消失点群へはどうやってもいかない場合があります。
画像:BOXを画面左端と右端に配置したもの。見た目は同じBOX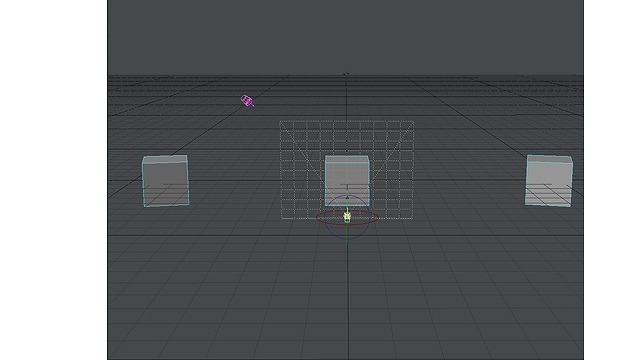
このような位置に置くと、どうやっても0度消失点群の線には到達しません。どういうことでしょうか?
実は0度の消失点群の縦線は、ワールド座標における「0度」なのです。ワールド座標というのは、文字通り世界の座標という意味で、この空間の中にある絶対的な座標を示しています。
この図を見ればわかるように、3つのBOXはそれぞれちょっと向きが違います。「自分から見た形状」はすべて同じなのですが、右のBOXはやや右外側を向いており、左のBOXはやや左外側を向いています。
今まで説明していた「BOXの回転角度」、左に15度下に30度とか説明していたこの回転角度というのは、実はこの「自分から見た角度」のことだったのです。この角度の値が同じなら、見た目の形はまったく同じなのですが、この図を見ればわかるように、同じ向きを向いてはいません。
このように「自分から見た目の角度」のことを「カメラ座標」といいます。
これに対し、下図はすべてのBOXが同じ方向を向いています。
画像:ワールド座標で同じ方向を向いているBOX3つ。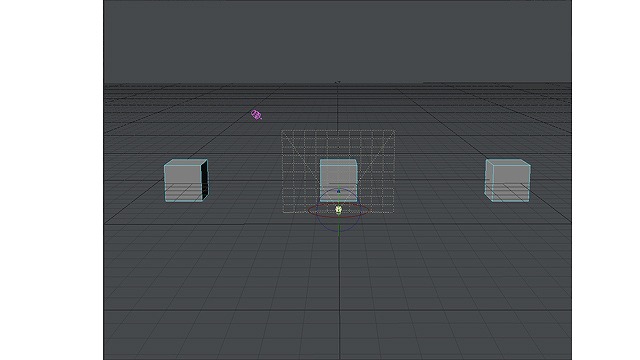
このように、見た目の形状は異なるけれども、すべてのBOXは同じ方向を向いており、この場合は「ワールド座標系で同じ角度である」といいます。
別の例を見てみます。以下の3つのBOXは、ワールド座標系ではすべて同じ、左30度回転しています。
画像:ワールド座標系で左30度回転させたBOXを3つ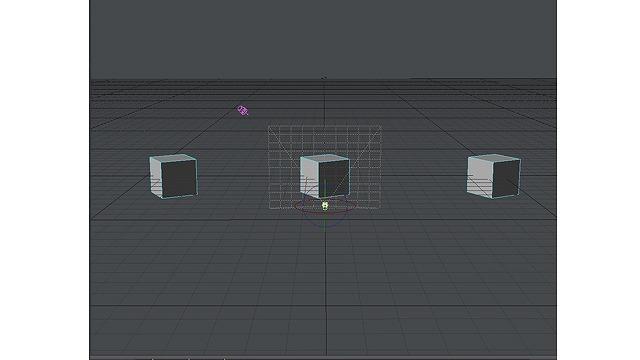
これらは真上から見るとこのようになっており、
画像:真上から見たBOX3つ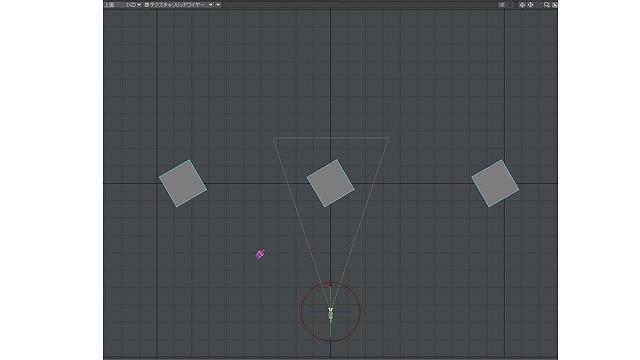
3つとも平行に並んでいるのがわかりますね。これらの奥行き線はすべて平行で、ちゃんと30度の消失点へ向かいます。
しかしこれらを図の「カメラ」から、それぞれのBOXを見るとどんな風に見えるでしょうか。まず真ん中のBOXは
画像:真ん中のBOX
普通に左に30度回転しているように見えます。では左のBOXを見てみると、
画像:左のBOX
これは逆方向に10度くらい回転しているように見えます。また右のBOXは
画像:右のBOX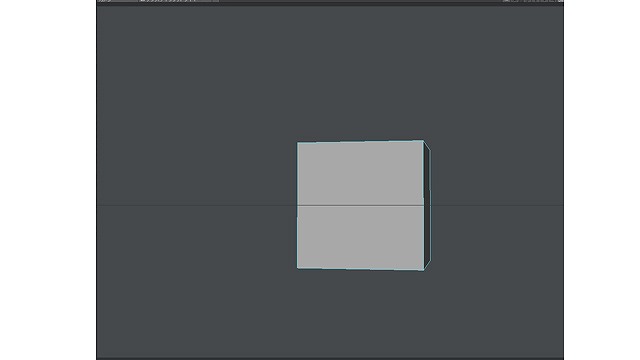
こちらは左80度くらい回転しているように見えます。
このように、ワールド座標系では同じ角度回転しているのに、カメラ座標系では異なる角度イコール異なる形に見えます。
私が今まで、「BOXを○○度回転させて……」といってきたのは、実はワールド座標ではなく、カメラ座標の話だったのです。
いっぽう消失点群の角度はワールド座標の角度を指します。たとえば「カメラ座標で30度左に回転」しても、それが30度の消失点に行き着くとは限りません。
BOXの計算
それではBOXの描画をしてみます(ただこの項でのやり方は煩雑すぎて実践的ではないので、理解しなくてもかまいません。その次に説明する短縮法のほうが実践的です)
BOXを仮に、奥行き左回転で15度、奥行き下回転でもさらに15度回転させたとしましょう。
画像:遠近なしで左15度、下15度回転させたBOX。奥面と前面の定義。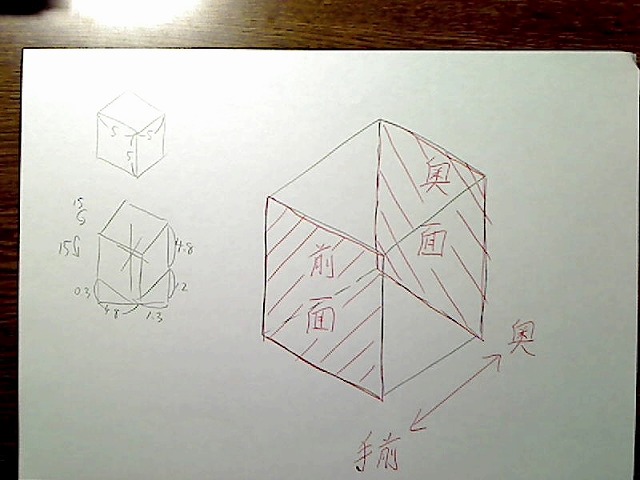
これの奥の面と前面についてですが、前面をどれだけ拡大するかを近似計算で求めてみます(近似計算なので完全に正確ではありません)
今からすることは、前面と奥面でどれくらい拡大縮小率があるかを知って、それをBOXに反映させることです。そのためにこの「拡大縮小度合い」が決まるようなほかの要素が画面内にある場合は、それにあわせなければなりません。
その要因の一つは「カメラと物体との距離」です。物体の前面と奥面の拡大縮小率は、カメラとBOXとの距離で変化します。近ければ近いほど拡大縮小率は大きくなります。
もし画面内に、カメラとBOXの距離を示す何かがあったら、それにあわせなければなりません。
そしてそれはすでに存在しており、「消失点群」です。消失点群がどれくらい画面に入ってくるかは、カメラの枠の取り方と関係しており、同時にこれはカメラとBOXとの距離も決めています(同じ大きさで人物を描いても、枠が小さく画面に入る消失点群が少なければ遠距離、枠が大きく画面に入る消失点群が多ければ近距離となる)
それでこの拡大縮小率は、消失点を参考にして決定することにします。
まず奥行き線について着目してみます。このBOXの辺を一つ、消失点まで引っ張ってみます。ただしこのときどこの消失点に引っ張るかは、カメラ座標ではなくワールド座標絵考えないといけません。カメラ座標で左15度、下15度と出しましたが、これをワールド座標に変換して消失点へ引っ張ります。
説明を簡単にするため、今回は画面の中央あたりに配置するので、カメラ座標とワールド座標は同じとします。したがってBOXの奥行き線は、右15度、上15度の消失点へ向かいます。
画像:BOXの奥行き線は右15度、上15度線の消失点へ向かう。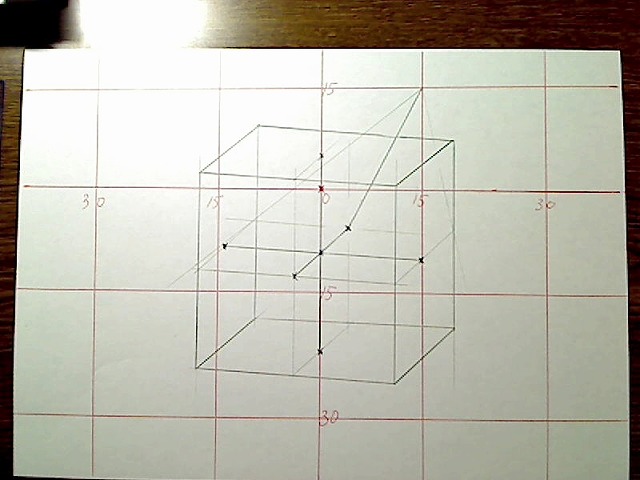
このBOXでは、とりあえず奥の面の大きさは変えず、前面だけ大きさを変更することとします。
奥の面の大きさを変えず、消失点へ向かわせ、前面へ向かって線を引きます。
奥行き線は遠近法の計算によって正確に表されていますが、前面を単に大きくするだけでは不足です。というのは、拡大は面だけで行われるだけでなく、立体的に行われるからです。
立体的に拡大されるので、前面は元のよりもさらに少し前に出てきます。どれくらいの割合で前に出てくるのか計算してみます。
消失点までの奥行き線の長さは、BOXの奥行き辺の2倍程度あります。
なので奥面の辺の長さに比べると、前面の辺の長さは相似の計算により、元の長さの2分の3程度になると思われます(完全に正確な計算ではありませんが)
それでBOXの奥行きの線の長さを、相似計算でこのように出します。
画像:奥行き線を各辺描画。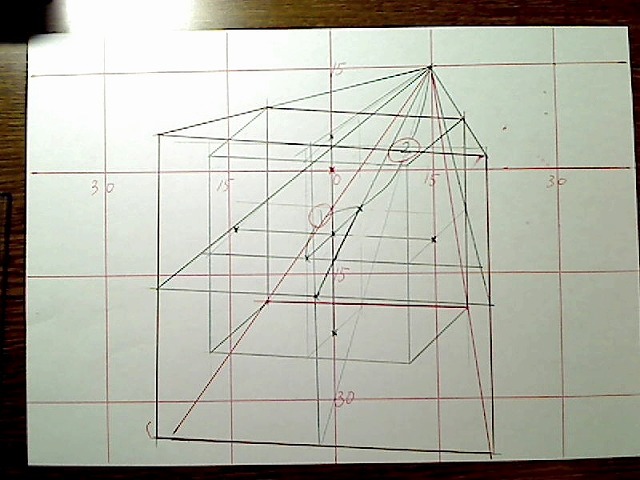
これで前面の四角形が描けました。
しかしこのような描き方では、そもそも計算自体が面倒な上、理屈も難しいです。また前面の四角形の形を正確に描画しにくく、定規でしっかり測らないと四角形の形がゆがんでしまいます。
また消失点が画面内にないと計算できません。たとえば横回転75度しているような場合、消失点が画面内に存在することはまずありえず、計算できなくなってしまいます。
ワールド座標とカメラ座標の変換も面倒です。そこでもう少し違う計算方法を提案してみます。
短縮法
この短縮法の概略ですが、まずBOXの消失点の位置を参考にして、奥面と前面の大きさの比率を相似計算で先に出してしまいます。
そしてその比率の値を使い、前面のBOXをその倍率で大きくするだけ、というものです。このやり方では消失点へ線を引っ張ったりはしません。
まず奥側の面に注目し、その面のちょうど中央の点を出しておきます。
画像:奥の面の中心点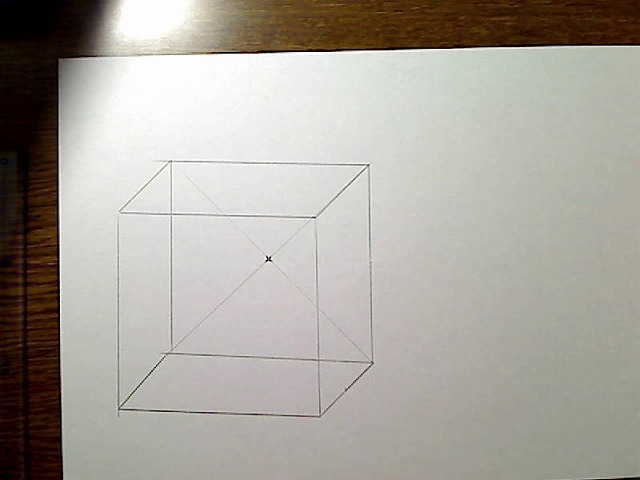
その縦横の辺の長さを出しておきます。図のように中心点からの縦長さをb、横長さをaとする。
画像:奥の面の縦の長さの半分をb、横の長さの半分をaとする。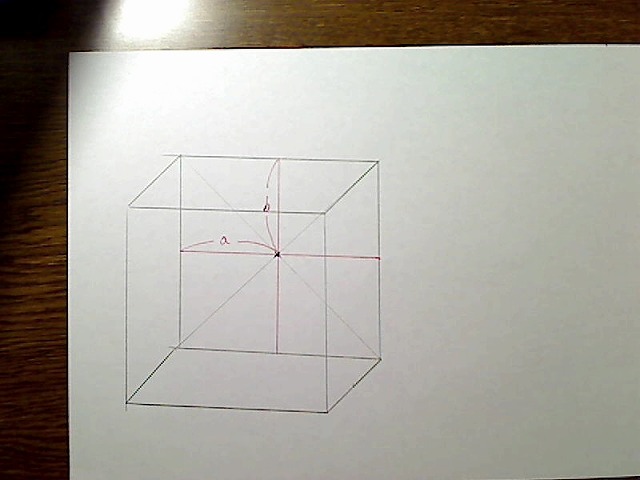
そしてBOXを描いてみて、その「奥行き辺」の長さを測ってみます。ここではとりあえず、その長さを1としましょう。
そこから消失点までの距離の比を出しておきます。だいたいでかまいません。ここでは4倍になっています。
消失点の位置は、BOXの回転角度をワールド座標に変換して出します。これも厳密にやると時間がかかるので、およそでかまいません。
画像:奥行き辺と消失点までの距離が奥行き線含めて4倍。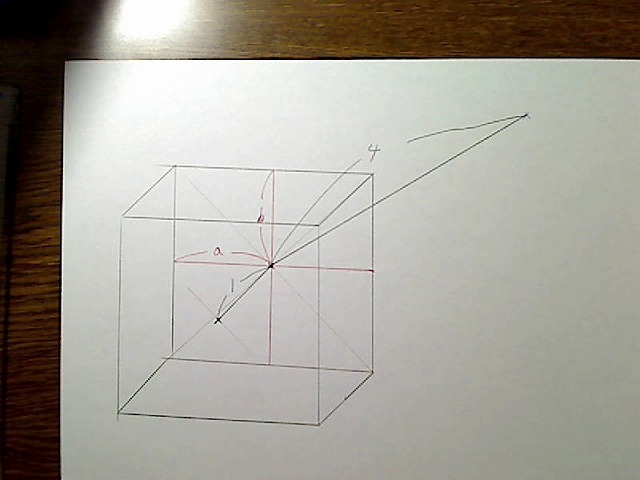
なお消失点は画面上になくてもよく、15度線の位置を設定していれば、60度でも75度でもBOXからの距離は計算で出せます。あまり厳密に計算すると時間がかかりすぎるので、大まかでかまいません。
この場合、相似計算により、前面の四角形の大きさは、理屈上では奥の面の四角形の4分の5倍になると考えます。
それでとりあえず、前面と奥面の比率は、この4分の5という数字を使おうというわけです。先ほどは消失点からBOXに線を何本か引っぱったりしましたが、これは面倒なので省略します。単に前面を4分の5倍するだけです。これならあまり時間もかからず、計算も簡単です。
それで前面の四角形の、横の辺、縦の辺を4分の5倍します。
同様に、奥行き辺も長くしなければなりません。そしてこのとき、奥行き辺の倍率は、1+4分の5を2で割った8分の9倍とします。この理由はややこしいので後で説明します。とりあえずこれで進めます。
この奥行き線を8分の9倍したところに中心点を取り、ここを拡大後の前面の中心点としましょう。
画像:奥行き辺を8分の9倍して前面の中心とする。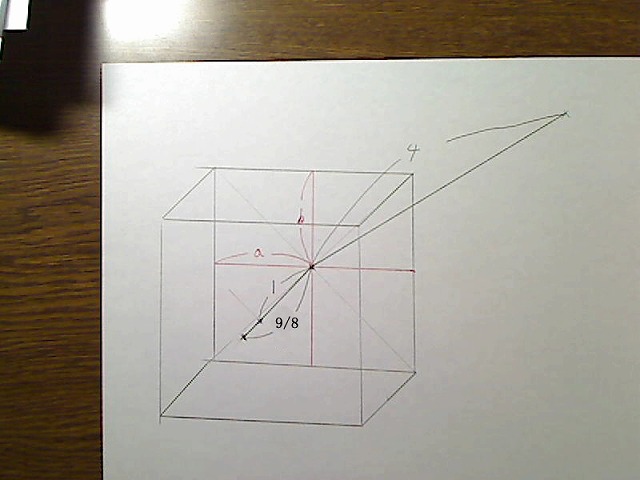
そこを中心に縦横に4分の5倍した四角形を描き、これを拡大後の前面とします。
画像:拡大後の前面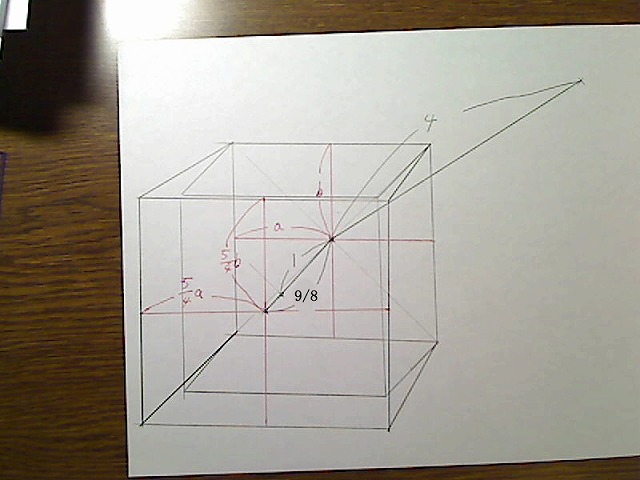
後は拡大前の前面を消せばBOXの完成です。
奥行き辺がなぜ8分の9倍なのか
先ほど、なぜか奥行き辺の倍率が、4分の5ではなく、1+4分の5を2で割った8分の9でした。この理由です。
ここでは前面の大きさは、奥面の大きさの4分の5倍としてやっています。縦と横の辺はこれでかまいません。が、奥行き辺に関しては、このすべての部分が4分の5倍であるとは限りません。
奥行き辺のみ「遠近」がついています。なので奥行き辺の、一番奥の辺りはまだ1倍程度の倍率で、こちらに向かってくるにしたがって少しずつ倍率が大きくなり、一番手前になると4分の5倍(1.25倍)になる、というイメージです。
イメージとして、奥行き辺を細分割し、たとえば6つに分割してみます。このうち一番奥の側はまだ1倍くらいでしょうか。しかしその一つ手前ではもう少し倍率が大きくなって、1.05倍程度になるとします。
さらに手前では1.1、さらに1.15,1.2、最後に1.25、というようなイメージになります。
画像:手前に来るにしたがって倍率が増えていくイメージ。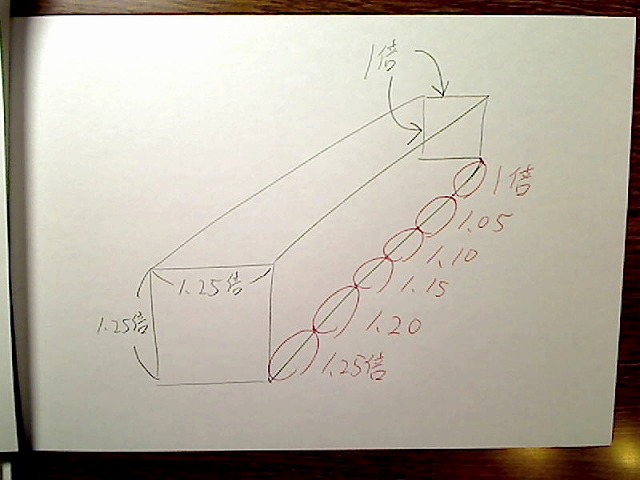
このように少しずつ倍率が拡大されてくるため、奥行き辺の長さを単純に1.25倍とすると、長くなりすぎて不自然に見えてしまいます。
この奥行き辺の長さは、これらの数字の平均値を取れば、およそそれっぽい値になるのではないでしょうか。そしてその平均値を取ると、(1+使うべき倍率)を2で割った値になります。
たとえばこの図の場合、
(1.00+1.05+1.10+1.15+1.20+1.25)÷4=1.125
で、
(1+1.25)/2=1.125
になります。
もっと細かく分割してみても同じで、たとえば
(1+1.01+1.02+1.03+……1.24+1.25)÷26=1.125
となります。
要するに、ちょうど真ん中の倍率を取るわけです。
こういう理由で、奥行き線だけは本来の倍率と元の倍率の中間の値、つまり「(1+その倍率)÷2」の値をとっておこうという考え方です。
消失点が画面外にある場合
消失点が画面外にある場合の計算をしてみましょう。
たとえばBOXが左に75度回転しているとします。
まず右15度線を設定しましょう。0度線からの長さが紙面上で5センチとします。
画像:0度線から15度線までの長さが5センチ。
右75度線はこれの約14倍なので、75度線は0度線から70センチのところにあるはずです。
画像:75度線までは70センチ。
これで先ほどと同じく、BOXを描きます。BOXは今回は一辺の長さが10センチの立方体で、これを左に75度、下に15度回転させたものとします。長さを計算し、紙面に描画します。
画像:BOXを描画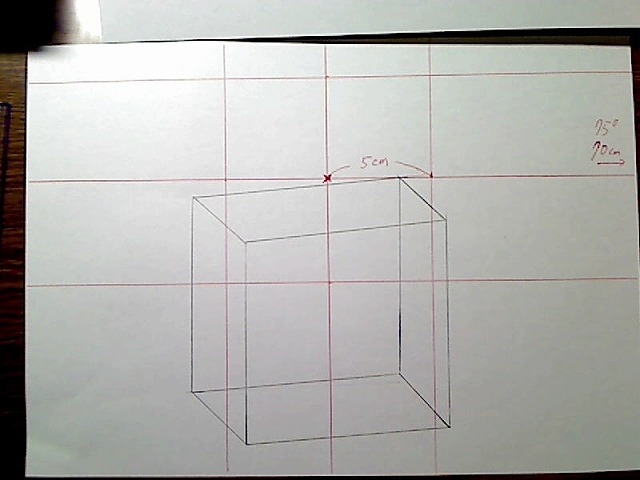
そして奥の面の中心をとり、奥行き線の長さを測ります。ここでは9.7センチでした。
BOXの奥行き線の、拡大前の長さは9.7センチということです。
画像:奥行き線の長さが拡大前は9.7センチ。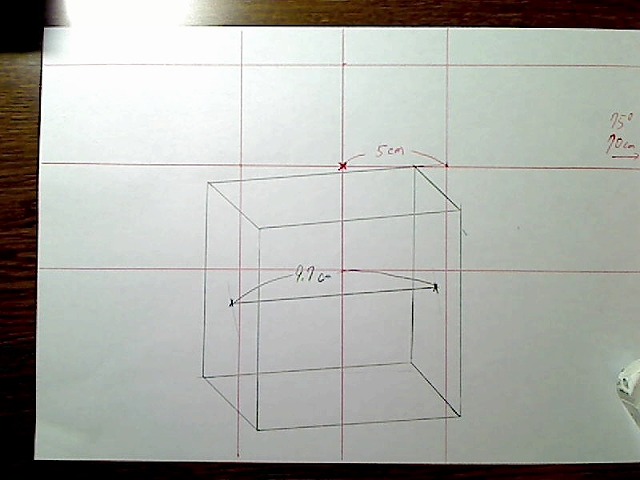
これで奥行き線と消失点までの長さの比は、9.7センチと66センチなので、6.8倍になります。相似計算により、前面の四角形は、奥の面の四角形の78/68倍(約1.15倍)となります。
そして先ほどと同様、奥の面の中心点から前面の中心点までの線を引きます。
奥行き線の長さは9.7×((1+1.15)÷2)で約10.4センチです。
画像:前面の中央点。奥行き線は10.4センチ。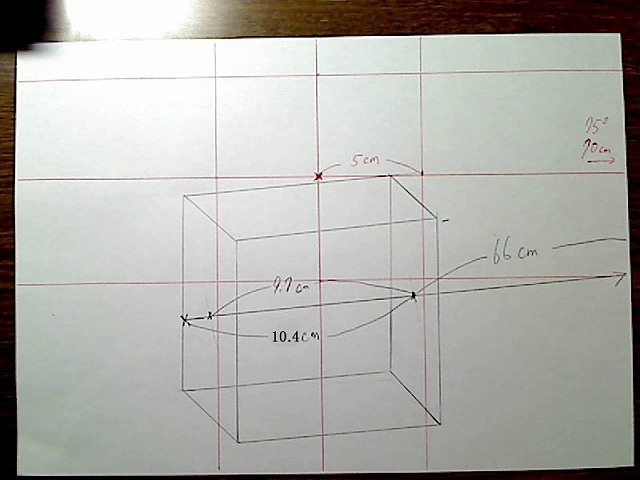
ここから縦の長さと横の長さを出します。元の長さの1.15倍の大きさの平行四辺形を描きます。
画像:前面の四角形を描画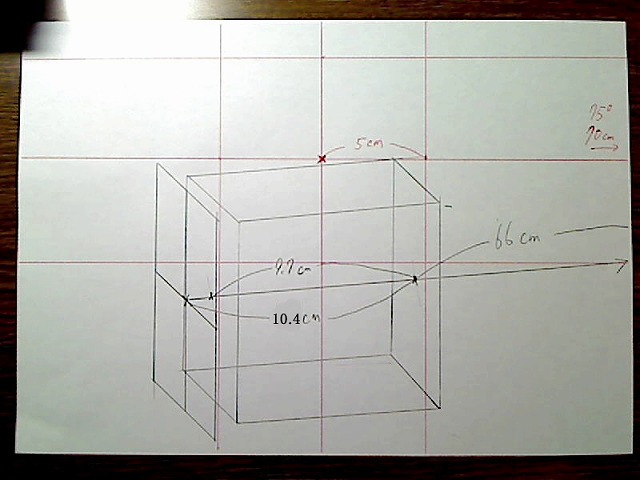
これにしたがって後は四角形を描くだけです。
画像:拡大後のBOXを描画。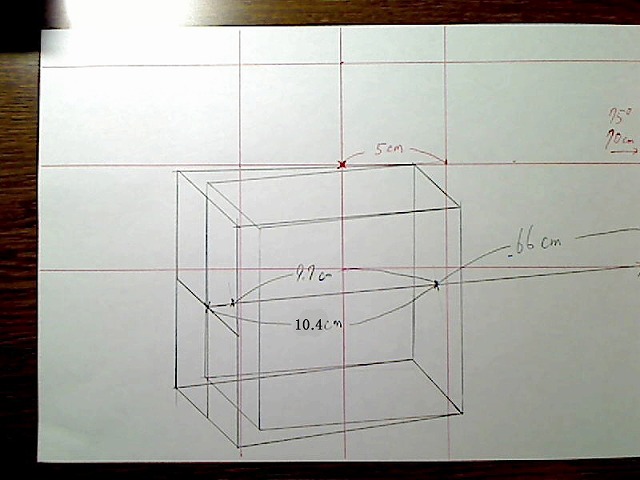
それにしても、75度回転させると、奥の面と前面の四角形は、ほとんど大きさに違いがありません。わずか1.15倍の違いです。
奥行き回転させても、大きく回転させると奥の面と前面はほとんど違いが見られなくなります。が、まったく同じ大きさにすると、やはり遠近がなくなってしまい、おかしな絵に見えることがあります。
なので不自然だと思ったら、1.15倍ではなくもう少し大きな値にしてもいいかもしれません。何度も述べているとおり、この拡大縮小率は、カメラと物体の距離によって異なるものです。
またこれに関しては、少々間違ってもふつうの人には「間違っている」ことすらほとんどわからないので、少しの数値の違いくらいは気にすることはありません。BOXの回転のときのように、「この数字でないと間違い」というような基準はないので、適当な倍率でやってもおかしく見えません。
数字を使わなくても、「およそこれくらいの倍率」と目測でやってもいいでしょう。
ただこの拡大縮小率は、消失点が近い位置ほど大きくなります。消失点が75度線の場合はわずかな拡大でいいのですが、15度線の場合は、もう少し前面を拡大しないといけません。拡大が足りないとやはり不自然に見えることがあります。