ところで「BOX理論」というのは、要するに体の各部の大きさを箱型で示し、それらを関節でつないで概形を求めようとするものです。
なぜ箱の形なのでしょうか?球形ではいけないのでしょうか?
よく頭部の描き方の説明で、頭部を球形にたとえて描いている講座がありますが、そのやり方ではいけないのでしょうか?
実は球形で概形を取る方法は、速く描くことはできるのですが、まるで正確には描けません。その理由を説明しましょう。
球形では正確に描けない理由
BOX理論では定規でBOXの縦、横、奥行きの長さを計算した上で描画に入るので非常に正確です。
またBOX内部のパーツについても定規で測定してから位置取りをするので、こちらも正確です。
これを球形にしてやってみますと、まず最初に球、つまり頭部の輪郭線を適当に手で描くわけですが、これで少しでも大きさを間違うと、頭部の大きさを間違うことになります。これはいけません。
少しでも球の縦の長さか横の長さ、あるいはきれいな円の輪郭をかけないと、やはりゆがんだ頭部になってしまいます。
せめて球の中心の縦長と横長を定規で測定するくらいのことはやったほうがいいでしょう。ただこれはBOX理論でも同じことをやっています。
画像:縦横の中心線と球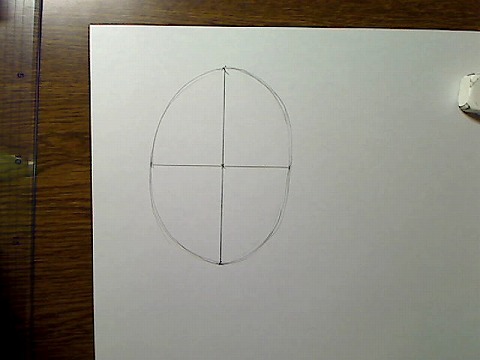
しかし正面から見た絵ならいいのですが、これが縦や横に回転すると困ったことになります。
たとえば頭部全体が右下を向いている絵を描くときも、球形を基本にして頭部の輪郭を描きます。
同じく左上を向いていても、やはり球形を基本にして描きます。
画像:球形で右下、左上を見ている図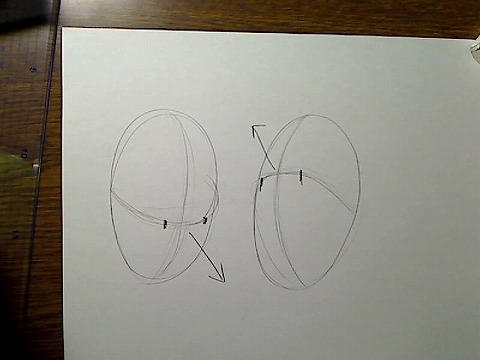
困ったことにこのやり方は「頭部は右上を向いていても左下を向いていても、球という同じ形をしている」という解釈になってしまいます。
実は人間の頭部は、およそ左右対称ではありますが、とても「球形」と呼べるような形はしていません。
顔の前面はパーツで複雑にデコボコしていますし、あごはとがっているし、頭部は上半分と下半分ではかなり形状が異なります。
それでも「だいたい球に近い」というだけなので、球形を基本に描いていると、厳密なところでさまざまに位置取りを間違えてしまいます。
簡易なマンガのキャラクターの絵なら、少々デッサンが狂ってもあまり気になりません。特に線画のみで詳細な陰影をつけない場合は、デッサンを多少間違えても不自然に見えないものです。
しかしこのウェブサイトでは、そういったわずかな間違いも許容せず、厳密なデッサンをやりたい方針なので、「だいたい球形」という指標ではなく、数値単位で各部分の位置をしっかり把握していこうというのです。
球を中心に考えていると、位置取りが不正確であり、厳密な形状の描画に関しては個人の裁量によることとなります。
ここではデッサンのカンが悪くても正確に描画する方法を追及していきますので、BOXを中心に考えるのです。
各部分の、キーポイントとなる位置の把握には、球形では困るのです。これは数学的に説明できます。
ある位置を正確に示す方法は?
空間の中である一点を正確に示すにはどうすればいいでしょうか?
ある人が「この位置は○○」と説明すれば、ほかの人でもその位置が完全に正確にわかるような、そういう説明のしかたがあるでしょうか。
中学か高校あたりで「空間座標系」というのを数学で習うようになります。X,Y,Zを使って空間を表すやり方です。
もっとさかのぼると、小学校のときの「正比例」の勉強で、X,Yの座標系が出てきます。
たとえばY=Xのグラフを描くと、ちょうど斜め45度の右上がりの直線のグラフになるでしょう。
このXY座標系にもう一つ次元を追加して、Zも加えます。こんな座標系です。
画像:XYZ座標系のXYZ軸のみ示す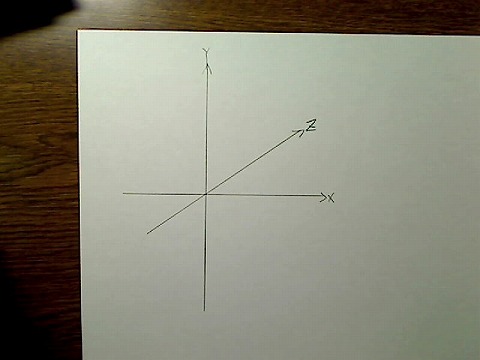
こういった空間で、たとえばX,Y,Z=(2,3,1)と示すと、空間の中でただ1点の位置が決まります。
画像:(2,3,1)の点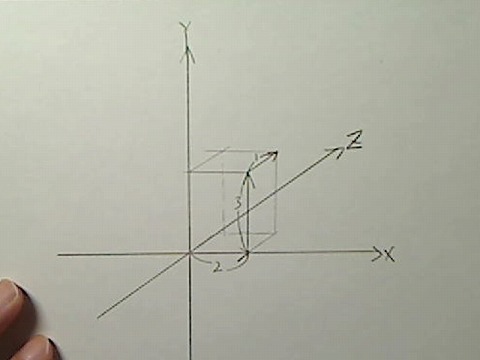
このようにX,Y,Z、言い換えれば「縦、横、高さ」を数字で示せば、空間の中の正確な一点を示せるということです。
さて、ためしに頭部を右下に回転させたややこしい構図を作ってみます。
この状態で顔面のパーツの位置を正確に描こうとします。するとこのようになります。
画像:右下を向いた顔面。目を描きこむ。目の位置の縦横高さの長さを示す矢印。
このようにBOXの表面を見ながら、高さや横の位置、奥行きもほぼ定規で測定して出せるというわけです。
BOXつまり長方形という形状によって、縦、横、高さを直線で示すことができます。直線で位置を示すために、定規で測定可能というわけです。
また、実はXYZ座標系のほか、ある点からの直線距離と角度によって示す「極座標系」という座標系もありますが、こちらの描画はややこしくなるので扱いません(角度の描画が必要になるので分度器が必要になります)