回転の理屈
ではまず、回転のイメージのつかみから始めましょう。
一つのBOXを正面から見たとき、横幅をa、奥行き幅をb、縦の長さをcとします。各辺の絶対長さを見るとこうなります。
画像:BOXの各辺の絶対長さ。横a,奥行きb,縦c、斜め上から見た図。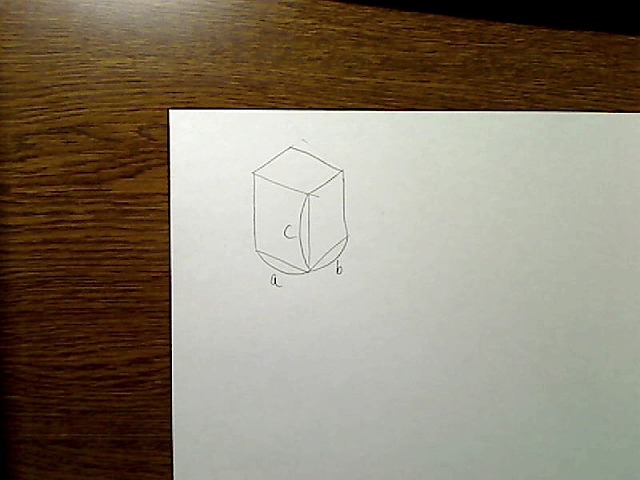
これを真正面から見た図と、真上から見た図はこうなります。
画像:BOXを真正面と真上から見た図。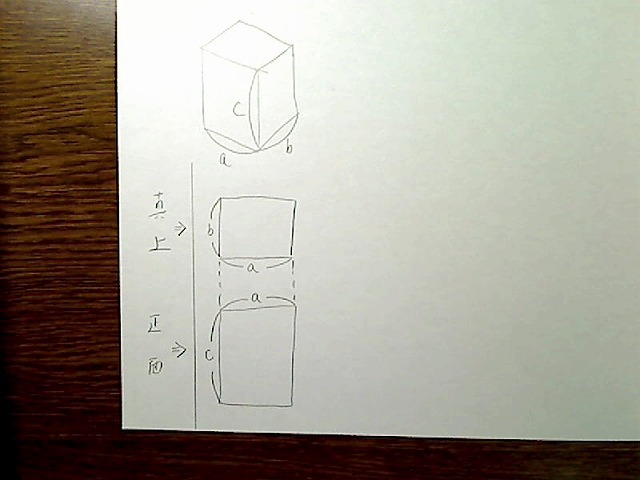
さて、これを奥行き横回転(左方向)へθ度回転させてみます。すると真正面と真上から見た図ではこうなります。
画像:BOXを横θ度回転、真正面図と真上図。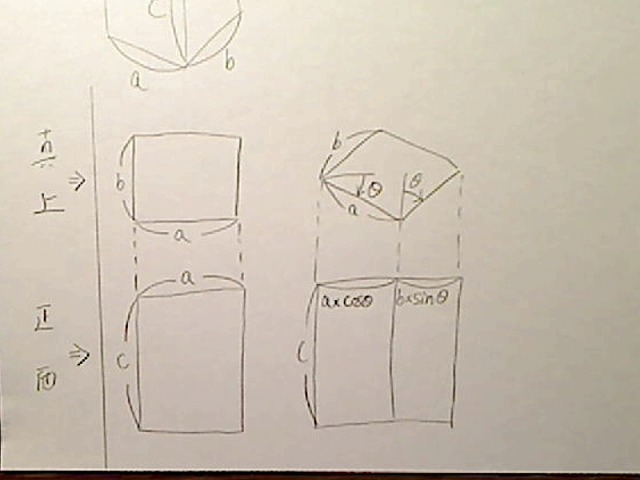
ここまでは前の章でやりました。これをさらに縦方向へβ度下方向へ回転させたものを、真正面から(カメラから)見るとこのような形になります。
画像:BOXを縦にβ度下へ回転、真正面図。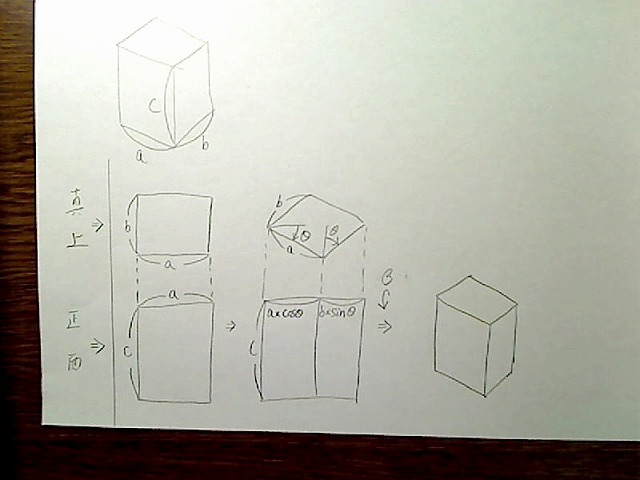
線だけで描いたのではわかりにくいかもしれません。3DCGの箱を用いて、同じ回転をさせてみましょう。
画像:3DCGでBOX、真正面→横回転→縦回転させたもの。
この中でどこの長さを求めたいのかというと、それぞれの辺の直接の長さではなく、紙面から見て縦の見た目の高さと横の見た目の幅です。斜め方向の長さを求めても意味がありません。図で表すとこうです。
画像:BOXの中の求めるべき長さ。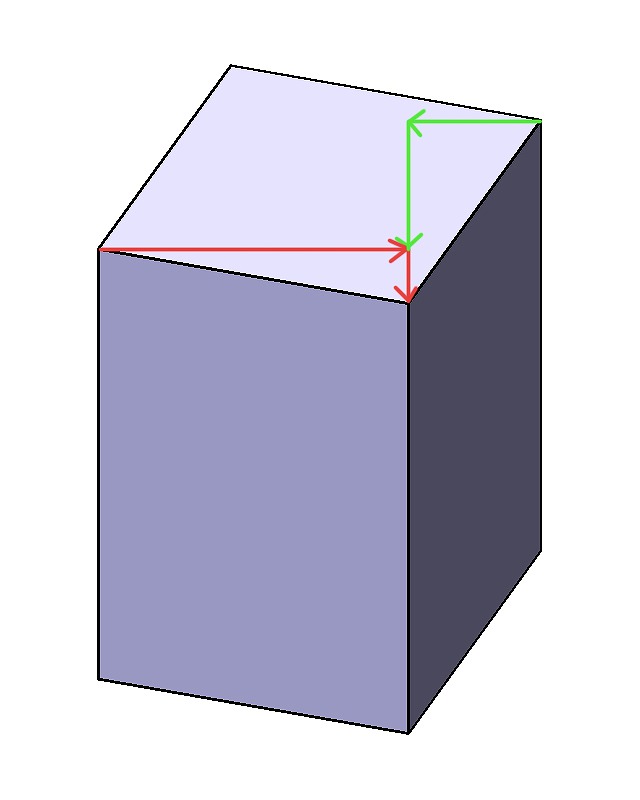
これらの長さがわかれば、定規で測って正確な線を描くことができます。
さて、横回転したときの各辺の見た目の長さは、先の章でやりました。このようになっています。
画像:BOX横回転直後の各辺の長さ。幅はa×cosθ、奥行きはc×sinθ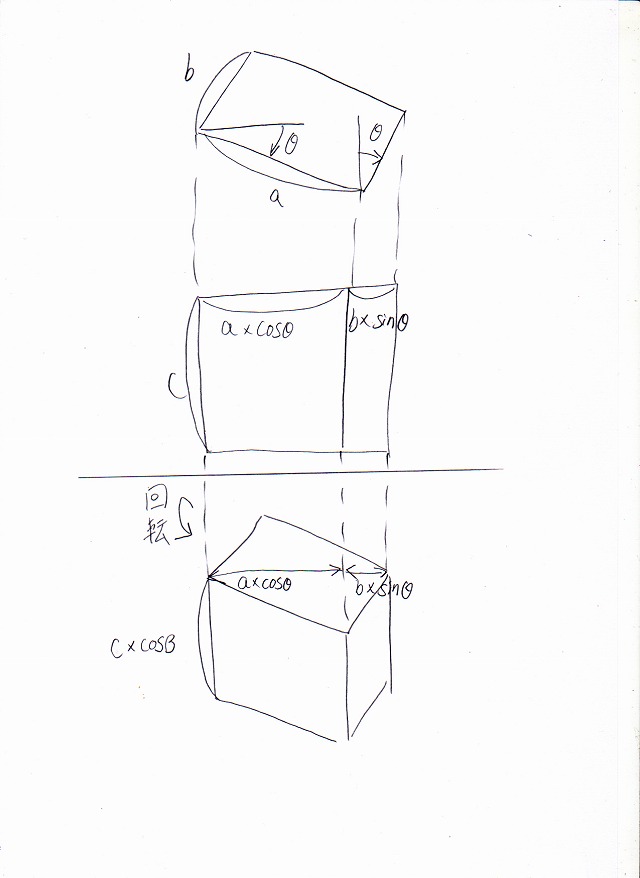
これを縦回転させた後ですが、まずこの2つの辺は、見た目のとおりで長さは変わりません。
出しやすいところから出していきましょう。縦の辺の長さは、cをβだけ回転させたものなので、
画像:縦の長さはc×cosβ
です。残りは2つだけです。ただこの2つがややこしいです。
まず、最初の横回転させた直後の真上図を見て、線の奥行き長さを求めます。以下の2つの図の左に示しました。
画像:求めるべき最後の2辺の見た目の長さ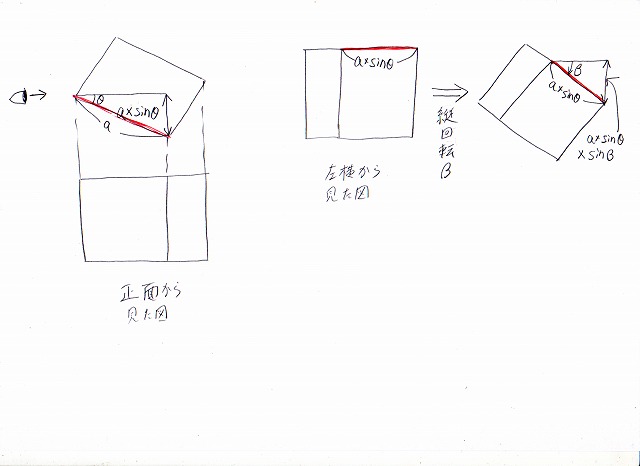
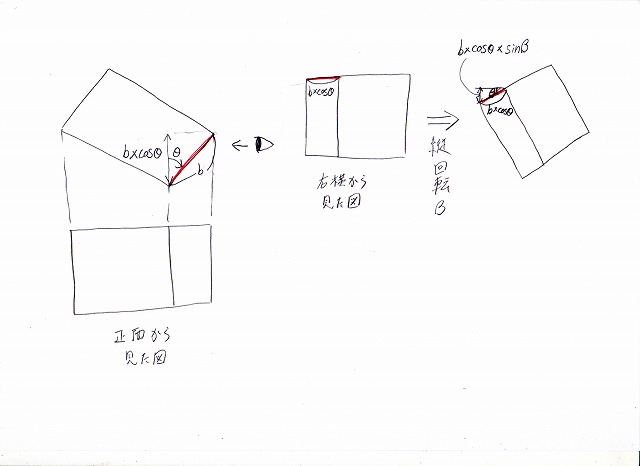
これら奥行きへまっすぐ向かっている線(a×sinθとb×cosθ)を、さらに縦回転β度させた後は、これらにさらにsinβをかけた値になります(2つ図のそれぞれ右)
よって求めるべき2つの部分の長さは、
aのほうがa×sinθ×sinβ
bのほうがb×cosθ×sinβ
となります。
画像:求めるべき最後の2辺の見た目の長さ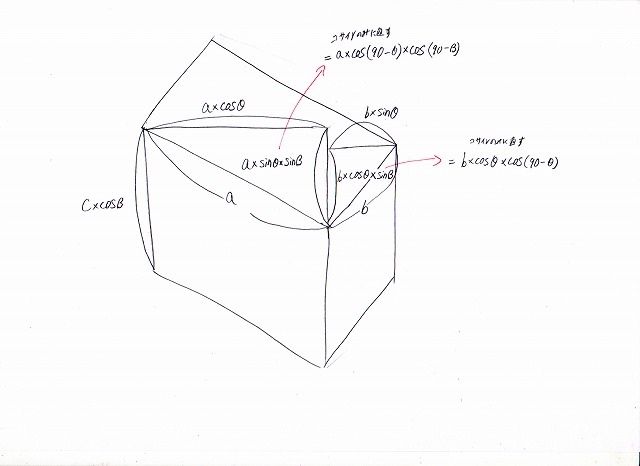
cosだけであらわすと、
aのほうがa×cos(90-θ)×cos(90-β)
bのほうがb×cosθ×cos(90-β)
となり、見た目は少々ややこしくなってしまいます。
それにしても、これだけ計算させられると手間がかかって面倒で、しかも途中で計算を間違う可能性もあります。
そんな計算をしているヒマがあったら、手書きでさっさと見当をつけて下書きしたほうが確実で早いかもしれません。
このあたりはなんともいえないのですが、要は数字の計算が面倒なだけなので、たとえば関数電卓で式を作っておいて数字を入れれば自動計算できるようにしておくとか、エクセルでやはり自動計算させるかしてしまうと、すぐさま正確な値を出すことができます。
それも面倒だ、やはりカンで描いたほうが速いのではないかと思われるかもしれませんが、私の場合、自動計算のプログラムを使うとカンで下書きするよりも速く描けました。
もっとも速く描く方法は、3DCGを使う方法です。3DCGは取り扱いが難しい感がありますが、いくつかの箱を描画して回転させるだけなら、覚えることはそれほど多くはありません。
3DCGの使い方さえ知っていれば、一度仕組みを作ってしまえば計算する必要すらないので、おそらくもっとも速く概形を描くことができるでしょう。私が最もおすすめする方法です。
自動計算プログラムの配布
この計算の面倒さを何とかしようと、自動計算するプログラムを作りました。
必要であればダウンロードしてください。
SpeedCalc.exeのzipファイル
SpeedCalc.exeのzipファイル
これはC++というプログラム言語で書かれたファイルです。Windowsパソコン上なら新旧問わず動作します。
エクセルのように、あらかじめプログラムをインストールしていないと動かない、という心配もありません。
プログラムファイルを起動すると、width,depth,height,横回転角度、縦回転角度を入力する画面になります。それぞれ横の長さ、奥行き幅、縦の長さ、1回目の横回転の角度(単位は度)、2回目の縦回転の角度(単位は度)を入力します。
画像:BOXの対応する長さ。斜め上から見た図。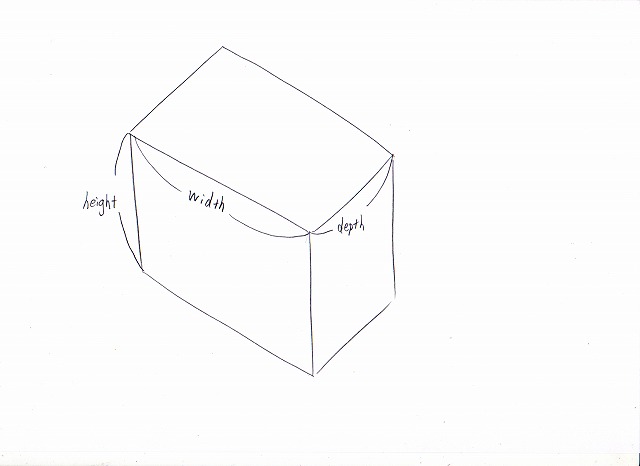
そして出てきた値と対応する長さは次のようになります。
画像:縦回転後の見た目の長さの対応図。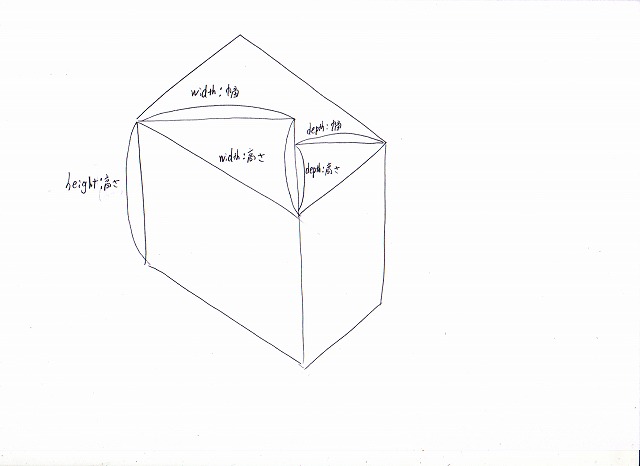
終わるときは右上の×印をクリックしてください。
なお、C++のソースファイルも一緒に入っています。
C++のプログラミングができる方は、このファイルを改造して別の計算プログラムを作ることもできます。