枠の取り方と消失点群の位置
絵画には「枠」という概念があり、実際に人間が見ている景色の一部を切り取っている状態になります。
消失点群というのは視界の中の特定の位置に存在しますが、画面の枠の取り方によって位置は相対的に異なって見えます。
画像:視界全体と枠の取り方。大きな枠と小さな枠と消失点群。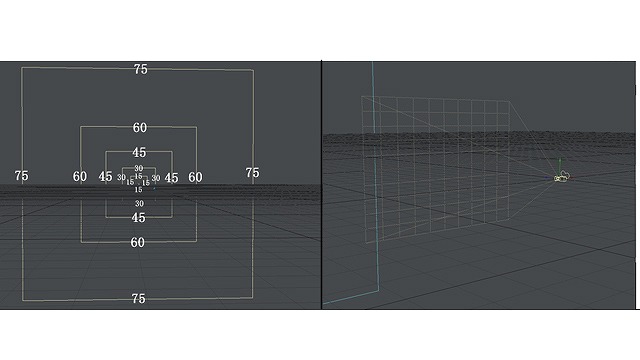
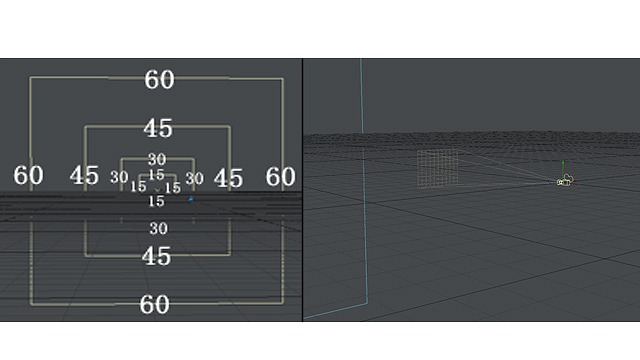
画像の絵の画面について、消失点群の縦線を見てみましょう(三角関数と同じく、角度については15度おきに出すことにします)
小さな枠では左右で最大値が60度までしか入っていませんが、大きな枠では左右で最大値が75度まで入っています(説明のために60と75という数字を使いましたが、通常の紙の大きさ、視界では、最大値は15〜30度まで、大きくても45度くらいまでしか入りません)
視界の中の、どのあたりで枠として区切るかによって、消失点群の位置は異なってきます。
なので、消失点群の位置というのは、画面の中で絶対的な位置が決まっているわけではありません。
絶対的な位置は決まっていませんが、相対的な位置(比率)は決まっています。
たとえば右15度の縦線の位置をまず決め、0度の位置からの距離を1とします。
画像:右15度の縦線の位置を、0度の位置から1の距離とする。
すると右30度の縦線の位置は、0度の位置からすると2.2の長さになります。
画像:右30度の縦線の位置は0度の位置から2.2の距離。
45度の位置は
画像:右45度の縦線の位置は0度の位置から3.9の位置。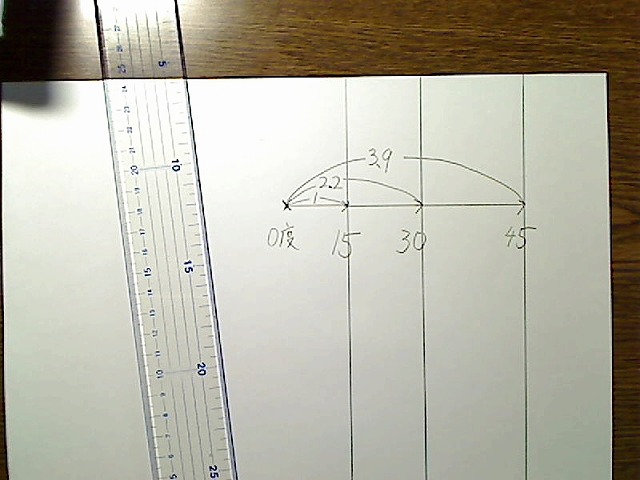
同様に、60度、75度の位置も決まります(60度は6.5倍、75度は13.9倍です)。理論上は最大で89.999……度まで出すことができ、90度では消失点は存在しません(90度になると奥行きがなくなり、真横の線になります。値は無限になります)
同様のやり方で横線(上下角度の消失点群)の位置も決めていきます。縦と横の距離は同じなので、横0度から横15度線までの距離は、縦0度から縦15度までの距離と同じです。
画像:縦15の線と横15度の、0からの距離は同じ。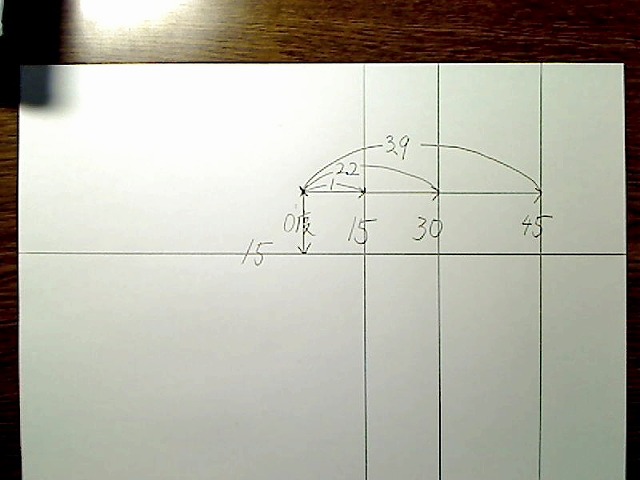
後も同様です。
画像:縦も45度まで描画。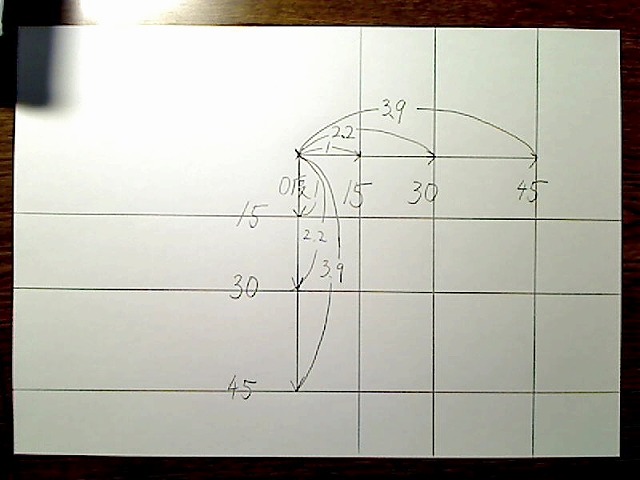
それ以外、上方向や左方向も対称です。
画像:上と左方向も描いてみる
これらの線は絶対的な位置が決まっているわけではありませんが、相対的な位置(比率)は決まっています。なので、最初に15度の位置を適当に決め、それにしたがってほかの線の位置を書いているわけです。
別に15度を最初に決めなくてもよく、75度から描き始めてもかまいません。要は線の比率的な位置があっていればいいわけです。
また私は15度おきに描いていますが、15という数字にこだわる必要もありません。
ところでこれらの倍率の数字(2.2、3.7、6.5、13.9)はどうやって計算したのでしょうか?その計算方法を次に見ていきます。
tan(タンジェント)
その前に三角関数のtan(タンジェント)について復習しておきましょう。
tanというのは三角関数のところでも少しやりましたが、図のような直角三角形で、tanθ=c/bとなります。
画像:直角三角形、斜辺がa、底辺がb、もう一つの辺がc。角度はθ。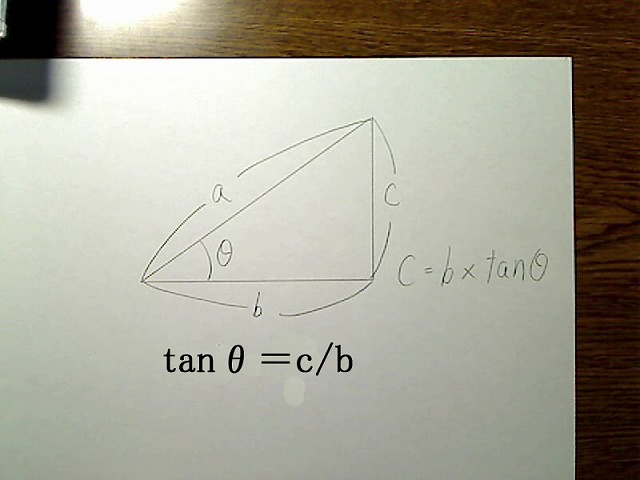
cの長さを出したいときは、b×tanθとなります。これを使用します。
消失点群の相対位置の数字計算
残りの消失点群の線の位置を計算で出してみましょう。
まず、遠近なしで真上から見た図を見てみます。
絵を見ている人の位置をPとします(目のマーク)。ここからまっすぐ奥のほうへ見ている場合、つまり縦横0度の消失点を見ている場合は、このようになります。
画像:真上から見た場合の消失点0度の位置。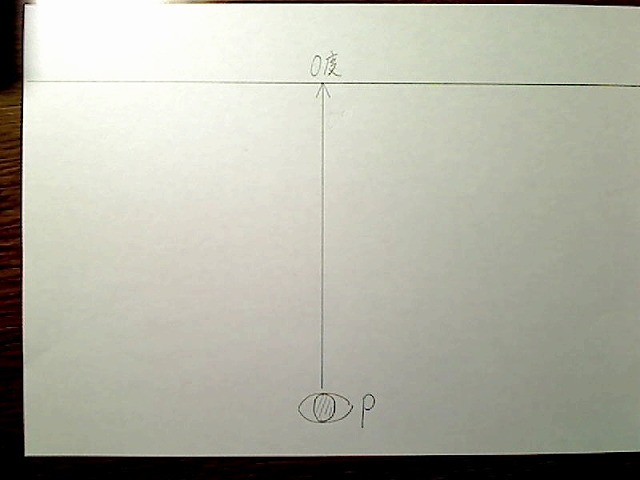
右15度の線を描いてみます。
画像:右15度の線。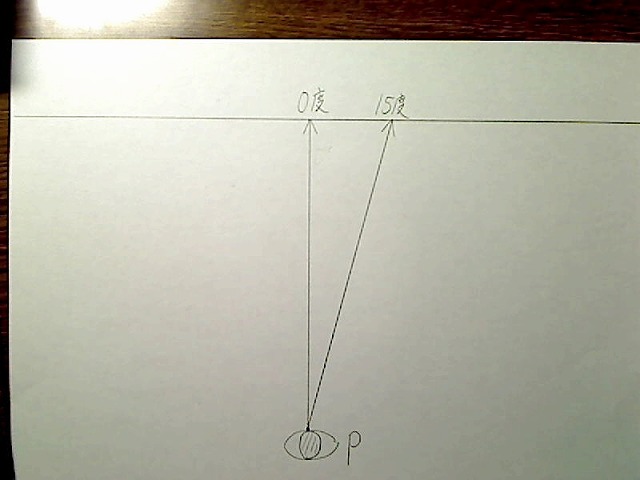
さてこのとき、目から0度の位置までの距離をAとすると、0度消失点から15度消失点までの距離は「A×tan15度」になります。
画像:A、15度の消失点までの距離はA×tan15度。
次に30度の位置を描いてみます。同様にして、消失点0度から消失点30度までの距離は、A×tan30度になります。
画像:30度消失点と、その距離。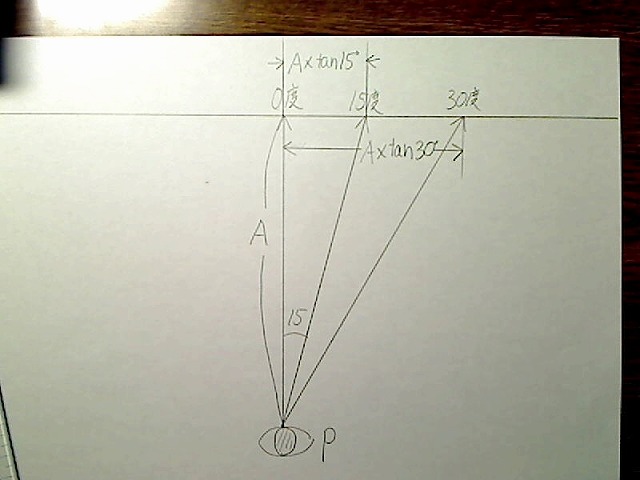
消失点0度から30度までの距離は、消失点0度から15度までの距離の何倍かというと、
(A×tan30度)÷(A×tan15度)
になります。つまりtan30度÷tan15度になります。
tan30度は約0.577で、tan15度は約0.268なので、この値は約2.15倍になります。
最初に右15度の位置を決め、これの長さを1とした場合、30度の位置はこれの2.15倍くらいになるわけです。四捨五入して2.2倍としましょう。
画像:右30度の線は右15度線の2.2倍。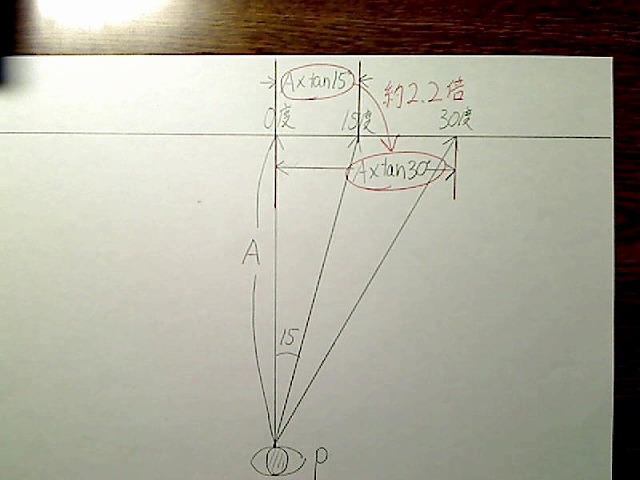
同じようにして、45度の縦線の位置は「tan45度÷tan15度」で、60度の位置は「tan60度÷tan15度」というふうにして、それぞれ距離を求めることができます。
これを75度まで、15度間隔で求めていきましょう。
画像:右75度まで15度おき。2.2、3.7、6.5、13.9
このような数字になります。左のほうはもちろん右と対称で、上下に関しても長さは同じになります。
画像:左右上下にすべて長さを出す。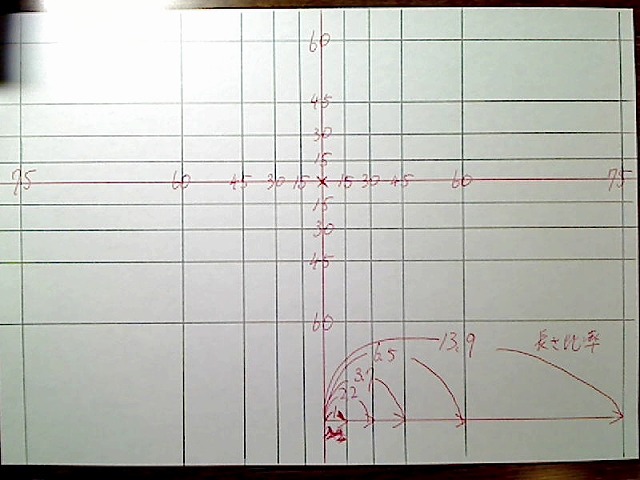
これで奥行き角度による消失点の位置は、すべて数値で出すことができました。後は奥行き線の角度によって、その位置に向かわせればいいだけです。
また今回は15度おきにやりましたが、10度おきにしたり30度おきにしたり、間隔を変えることもできます。
その場合は計算式を、たとえば10度おきの場合は最初に10度の線を定め「tan20度÷tan10度」「tan30度÷tan10度」のようにして残りの位置を求めていけばいいでしょう。
理屈がわからない場合
理屈がよくわからない場合、まずは画面の中心あたりに原点を取ります。画面の中心で、少し上あたりが妥当です。
ここから画面全体に十字の線を引きます。ここが0度の消失点群です。
説明のため画像は赤のボールペンで描いていますが、後で消せるように鉛筆で書いたほうがいいでしょう。
画像:遠近の原点。
次に15度の消失点群を画面の適当なところに描きます。中心から3分の1から2分の1あたりが妥当な場所です。
消失点群は正方形の形をしており、これらは「自分から見て15度奥行きのところへ向かう線はここへ向かう(消失点になる)」というものです。
画像:15度の消失点群。上下左右。
30度の消失点群の位置は、原点から15度線の2.2倍のところにあります。そこで同じように線を引きます。
画像:30度の消失点群。上下左右。
これ以降は画面外になるので、「だいたいこの位置」程度で考えておいてもいいでしょう。
45度線は15度線の3.7倍、60度線は6.5倍、75度線は13.9倍の位置にあるので、およそ見当をつけて消失点の位置として使うといいでしょう。
最初の15度の位置はどのようにして決めるのか
最初の15度の位置はどのようにして決めるのでしょうか?何か法則でもあるのでしょうか?
最初に説明しましたが、この位置は画面の枠の取り方によって決まります。
ところで「枠」とは何でしょうか?「枠」の概念をもっと厳密に考えてみます。
私たちは絵画の枠というのをまるで自分の視界のように捕らえていますが、枠というのはその視界の中の、一定の部分を切り取って写している状態です。
画像:視界と枠。
仮に目の前に箱があるとします。このとき枠の取り方を2種類、大きいものと小さいもので取ってみます。
画像:目の前に箱、小さい枠と大きい枠。3DCGで。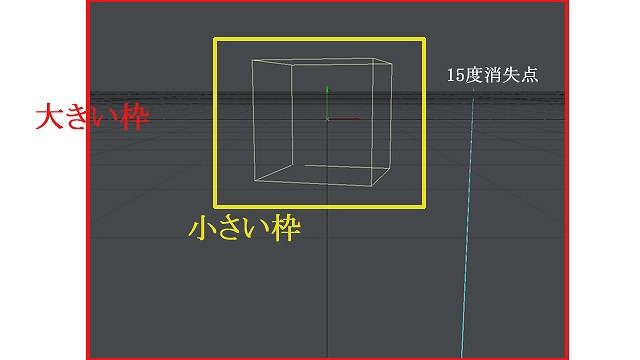
小さい枠では15度線は画面の外側にはみ出てしまいますが、大きい枠では画面の中に収まっています。
では、このような図はどうでしょうか。
画像:ズームファクターは同じでカメラを接近させたもの。
これはカメラを先ほどよりもさらに近づけてみたものです。先ほどは「遠くから画面を一部切り取っていた」のですが、これは視界の広さは同じで、カメラを接近させただけなのです。
BOXの見かけの大きさ自体は、先の「小さい枠」のときのと同じくらいの大きさに見えますが、見え方がずいぶんと違います。BOXをよく見ると、BOXの奥側の面と手前側の面の、いわゆる遠近の拡大縮小率が、先ほどよりも大きくなっています。カメラが近づくと、遠くのものがより小さく、近くのものがより小さく見えます。
ここで注意すべきことですが、先ほどの「大きい枠」のものと、視界の広さ自体は変わっていません。なので15度線はちゃんと画面内に収まっています。
でも先ほどの「小さい枠」のほうでは、画面内に15度線が入っていませんでした。これは視界自体を狭く取ったからであり、「遠くから見ているが枠を小さく切り取った」からです。
同じ範囲を写しているのに、枠の取り方とカメラの距離によって、このように15度線の位置(消失点群の位置)が変わるわけです。
あなたが人物画を描くときは、おそらく画面いっぱいにちょうど人間が納まるように人体を描画しようとするでしょう。
そのとき消失点群が画面にあまり収まらないように描くと、「視界が狭い」ことになります。視界が狭いというのは、いわば筒のようなものを通して対称の物体を見ているような状態です。なので視界が狭く、かつ至近距離から見ている場合、普通は体の一部しか見えないことでしょう。視界が狭いのに体が全部見えるということは、かなり遠くから見ているということになります。
つまり消失点群が画面に入りきらず、たとえば15度あたりまでしか画面に入りきらないような画面で、しかも人物が画面いっぱいに描かれているような場合、「かなり遠くから見ていて、視界が狭い(視界の一部を切り取ったような)」という状態になります。
一方、消失点群が画面にかなりたくさん収まっているような場合、45度くらいまで画面の中に入っているような画面だと、視界が広い状態になります。
視界が広くて画面いっぱいに人物が描かれていると、接近して人物を見ているような状態になります。
どのように消失点群を取っていくかは自由なのですが、それらの特徴を踏まえていることは重要です。
同じように画面いっぱいに人物を描いたとき、
視界が狭い(消失点群があまり入らない)と、遠距離から見ているような図になり、遠近の拡大縮小はあまりつきません。たとえば人物の腕をこちら側へ伸ばしているような場合、手はあまり大きく描かれません。迫力はありませんが、体の形状はあまりゆがまないので、ボディラインはきれいに見えます。
画像:遠距離から見た図。腕をこちらへ伸ばしている。遠近のゆがみが少ない。
視界が広い場合(消失点群がたくさん画面に入っている)、近距離から見ているような図になるので、人物の腕をこちらへ伸ばしたりすると遠近の拡大縮小が大きくなり、迫力のある図になります。しかし体の形が遠近で大きくゆがむので、顔面を大きく見せるような構図では、鼻や口が大きくなったりして不恰好に見えてしまいます。体のラインのゆがみも大きく、ボディラインの美しさよりも迫力を重視した構図といえるでしょう。
画像:近距離から見た図。腕をこちらへ伸ばしている。遠近のゆがみが大きい。
そのとき消失点群を画面内にたくさん収まるように描くと、それは「視界が広い」ことを意味します。
理屈がよくわからなければ、とりあえず
「同じように人物を画面いっぱいに描いた場合、視界が狭いほど(消失点群がより広がっているほど)遠距離から見た図になり、視界が広いほど(消失点群が狭く集約されているほど)より近距離から見た図(迫力のある図)になる」
と覚えておいてください。
0度の位置の決め方
消失点群の0度の位置、つまり「真正面を見たときの消失点」はどこになるのでしょうか?単に画面の中央でいいのでしょうか?実はこれも決め方があります。
画面の枠というのは、私たちの視界を模倣したものです。
そして視界には見える範囲の限界の角度があり、この限界角度まに比例して枠の大きさを決める、と考えるのがふつうです。
3DCGで見てみましょう。カメラを見てみると、このようになっています。
画像:3DCGでパース視点、カメラの枠が表示されている。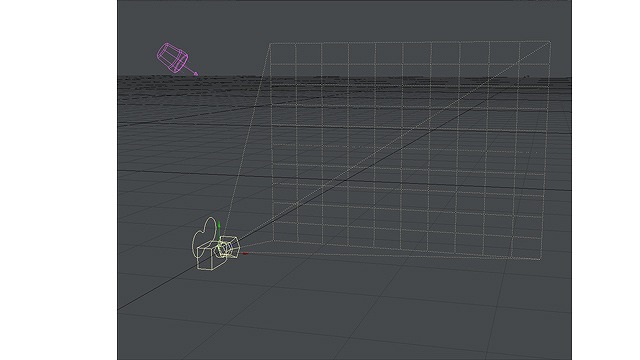
人間の視野はこんな感じです。それで人間の目の限界の角度はどれくらいでしょうか?
これは自分の目で試してみるとわかります。真正面を見ているとき、上下左右とどれくらいの角度まで見えるでしょうか?
やり方として、自分の視界外から少しずつ指を視界に入れていってみてください。どれくらいの角度から見えるようになりますか?
自分でやってみるとわかりますが、だいたい上は30度、下は60度、左右とも80度くらいです。
イメージで描くと、こんな感じです。
画像:左右の視野限界、上下の視野限界。0度からの直接の長さが画面の長さ。画面の長さ(0度消失点から視野限界消失点までの長さ)をx、目から0度消失点までの長さをaとする。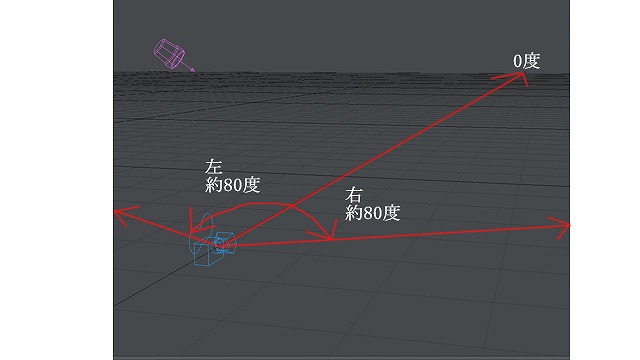
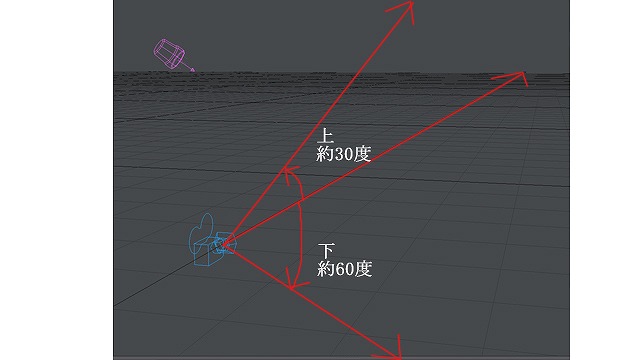
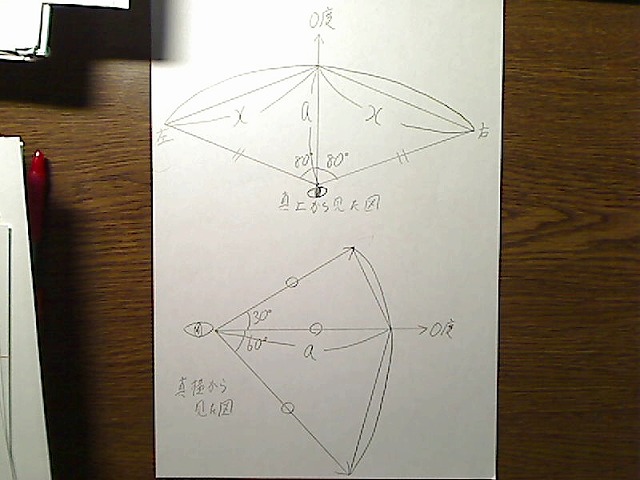
「画面の見た目の長さ」は、図のxの長さとしましょう。視野の面は球面を切り取ったような形をしています。
三角形の内角の和が180なのを利用し、三角関数を使って次のように、左右の画面の長さを限界角度80度として出してみます。
中央で三角形を2つに分けると、分けた線の長さがa×sin80度になります。
画像: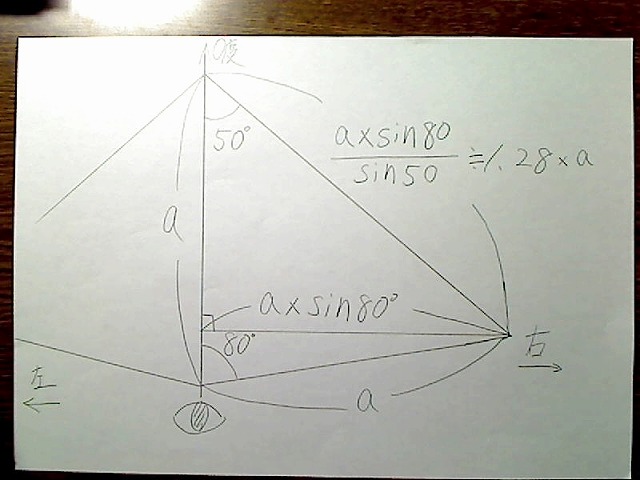
同じように上下も出してみます。
画像: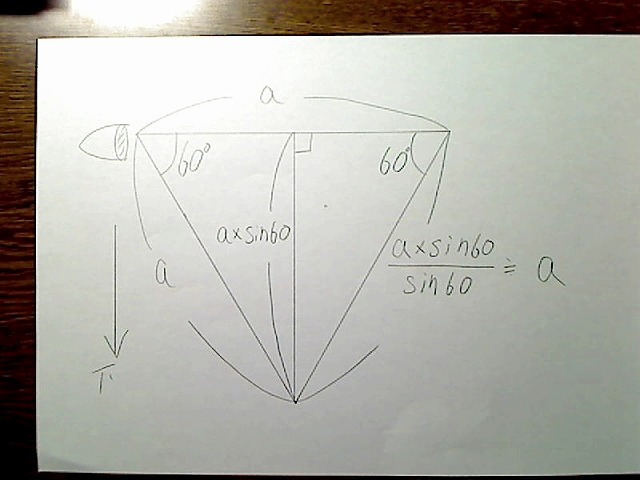
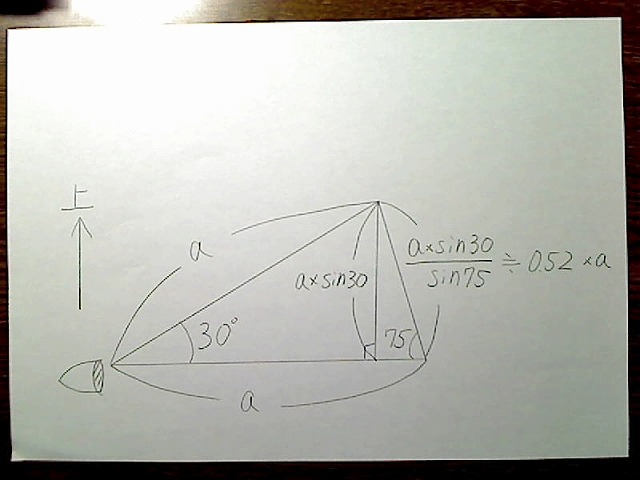
これよりそれぞれ比率を取ってみると、左右の長さはそれぞれ1.28、上は0.52、下は1.0となります。
よって、画面はこの長さで区切るとちょうどよさそうです。
それで消失点群の0度の位置ですが、まず左右に関しては「左右の中央」で問題ないでしょう。問題は上下の長さです。
上が約0.5で下が1なので、上に3分の1の点が、0度の点だと思われます。画面の0度の点をこのように取ってみます。
画像:0度の点を取る。
いかがでしょうか。0度の点は現実の風景でいえば、真正面を見ているときの地平線の位置になります。
ちょうど感覚的にもこれくらいではないでしょうか?
またこの紙では、紙の縦横比が最初から決まっていたのでこうなりましたが、比率的に左右が1.28、上0.52、下1.0とすると、A4の紙よりももう少し横長になります。
画像:比率そのままの四角形と中心点。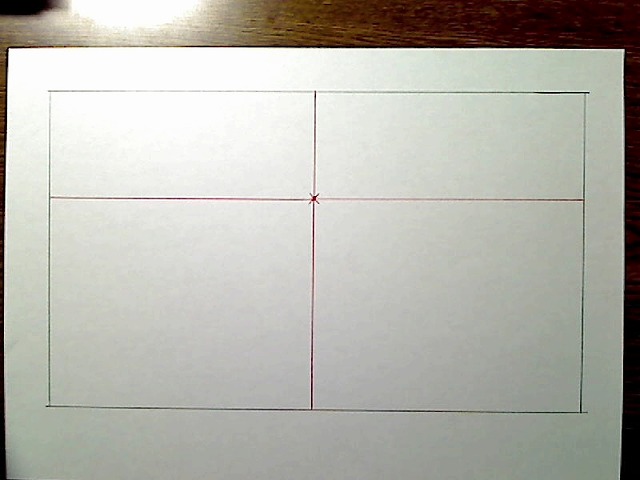
視野の球面について
先ほどは人間の視野の面を球面として計算しました。これは平面ではないのでしょうか?
画像:視野を平面とした場合の視野限界のイメージ。
しかしこのように設定してしまうと、横の長さはa×tan80度となり、5.6という大きな値になります。これを画面の大きさに反映させるとあまりにも横長になってしまいます。
画像:視野面を平面にした場合の画面の長さ。非常に横長。
これではいくらなんでもおかしいということで、視野面は球面にして計算しました。こちらのほうがしっくりくると思います。
理屈がよくわからない場合
これもややこしい数学を使って計算してしまったので、理屈を理解するだけでも大変です。
しかしこれは理屈を理解する必要はなく、使い方も難しくありません。応用するための数字を証明問題のように計算してみただけで、絵を描くときにこのような理屈を使う必要はありません。
絵を描くときは、真正面を見た場合、地平線の上下位置については、画面の上から3分の1の位置にある、ということだけ覚えておけば十分です。
画像:地平線の上下位置、上から3分の1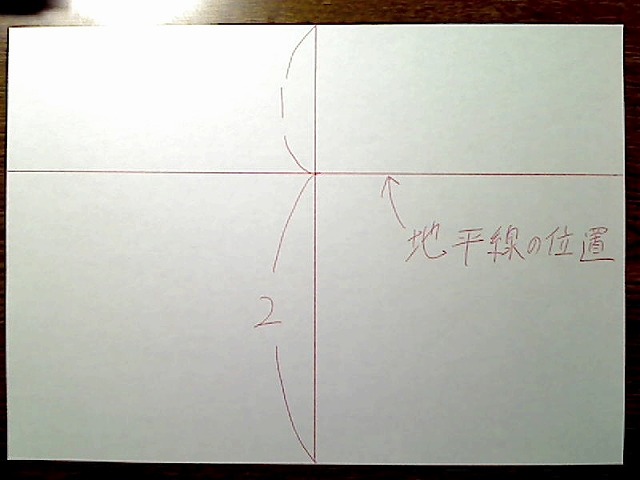
視野角度が球面だの平面だの、ややこしいことをいいましたが、これも覚える必要はありません。
視野角度が上に狭い理由
人間の視野は、自分で試してみるとわかりますが、上には狭いです。30度くらいしか見えません。
なぜでしょうか?どうやら人間にとって、上よりも下のほうが重要なようです。
おそらくは原始的な進化の理由で、上方向はあまり重要ではなく、下のほうが重要だったと思われます。
狩猟時代、上方からは攻撃を受けたり攻撃を仕掛けたりすることはあまりなく、下のほうにより注意を置かなければならなかったのが理由だと思います。
たとえば学校などで、2階や3階の窓から地上にいる友人に手を振ってみても、案外気づかないものです。人間は上の視界に関しては弱いようです。
画面の大きさ(縦横比率)の設定
このように画面の長さを視野角度で計算してみると、画面の縦横比率をできるだけ視野角度に近づけることで、より自然な枠を再現できます。
横の全長さは2.56で、縦は1.52です。横÷縦は、1.68になります。この比率に近づけると、より人間の視野に近く、自然に見えるのかもしれません。
たとえばパソコンのモニタの画面は、ずっと昔は縦480ピクセルで横640ピクセルでした。これの横÷縦は、約1.33です。
最近は横長になってきて、たとえば1920×1080などがあります。これの横÷縦は約1.77です。
A4のコピー紙は縦297ミリ、横210ミリです。この場合は約1.4です。
しかしこの比率は、発表する媒体によって制限されるかもしれません。動作サイトなどは、最近では1.77の横長の比率に移行しつつありますので(2015年時点)、画面の比率を自分で決められない場合はそれにあわせるしかありません。